Translate this page into:
Optimal perturbation iteration method for Bratu-type problems
⁎Corresponding author. n.bildik@cbu.edu.tr (Necdet Bildik)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
In this paper, we introduce the new optimal perturbation iteration method based on the perturbation iteration algorithms for the approximate solutions of nonlinear differential equations of many types. The proposed method is illustrated by studying Bratu-type equations. Our results show that only a few terms are required to obtain an approximate solution which is more accurate and efficient than many other methods in the literature.
Keywords
Optimal perturbation iteration method
Perturbation methods
Bratu-type equations
1 Introduction
Many nonlinear differential equations are used in many scientific studies and most of them cannot be solved analytically using traditional methods. Therefore these problems are often handled by a broad class of analytical and numerical methods such as Adomian decomposition method (Adomian, 1988; Deniz and Bildik, 2014), Taylor collocation method (Bildik and Deniz, 2015), differential transform method (Bildik and Konuralp, 2006), homotopy perturbation method (Öziş and Ağırseven, 2008), variational iteration method (He, 2003). These methods can give accurate solutions to nonlinear problems but they have also some problems about the convergence region of their series solution. These regions are generally small according to the desired solution. In order to cope with this task, researchers have recently proposed some new methods (Marinca and Herişanu, 2008; Liao, 2012; Idrees et al., 2010). Perturbation iteration method is one of them and has been recently developed by Pakdemirli et.al. It has proven that this method is very effective for solving many nonlinear equations arising in the scientific world (Aksoy and Pakdemirli, 2010; Aksoy et al., 2012; Şenol et al., 2013; Dolapçı et al., 2013; Khalid et al., 2015). In the presented study, we construct a new optimal perturbation iteration method which is applicable to a wide range of equations and does not require special transformations. In order to show the efficiency of the proposed method, we try to solve Bratu initial and boundary value problems which are used in a large variety of applications, such as the fuel ignition model of the theory of thermal combustion, the thermal reaction process model, radioactive heat transfer, nanotechnology and theory of chemical reaction (Doha et al., 2013; He et al., 2014; Raja, 2014).
2 Perturbation iteration method
Pakdemirli and his co-workers have modified the well-known perturbation method to construct perturbation iteration method (PIM). PIM has been efficiently applied to some strongly nonlinear systems and yields very approximate results (Aksoy et al., 2012; Şenol et al., 2013). In this section; we give basic information about perturbation iteration algorithms. They are classified with respect to the number of correction terms (n) and with respect to the degrees of derivatives in the Taylor expansions (m). Briefly, this process is represented as PIA ( ).
2.1 PIA (1,1)
In order to illustrate the algorithm, consider a second-order differential equation in closed form:
Substituting (2.2) into (2.1) and then expanding in a Taylor series gives
Rearranging Eq. (2.3) yields a linear second order differential equation:
We can easily obtain from Eq. (2.4) by using an initial guess . Then first approximation is determined by using this information.
2.2 PIA (1,2)
As distinct from PIA (1,1), we need to take
to obtain PIA (1,2). In other words, second order derivatives must be taken into consideration:
Note that all derivatives and functions are calculated at . By means of (2.2) and (2.6), iterative scheme is developed for the equation under consideration.
3 Optimal perturbation iteration method
To illustrate the basic concept of the optimal perturbation iteration method (OPIM), we first reconsider Eq. (2.1) as:
After Eqs. (2.4) and (2.6) in the solution processes for PIAs (1,m), we offer to use the formula
The following algorithm can be used for OPIM:
a) Take the governing differential equation as:
b) Substitute (2.2) into the nonlinear part of (3.4) and expand it in a Taylor series:
c) After finding
for each algorithm as in PIAs (1,m), substitute it into Eq. (3.2) to find the first approximate result:
By using initial condition and setting
yields
Using Eq. (3.8) and repeating the similar steps, we have:
d) Substitute the approximate solution
into Eq. (3.4) and the general problem results in the following residual:
Obviously, when
then the approximation
will be the exact solution. Generally it doesn’t happen, especially in nonlinear equations. To determine the optimum values of
; we here use the equations
The constants
can also be defined from the method of least squares:
4 Applications
Example 1. Consider the following nonlinear differential equation (Wazwaz, 2005):
4.1 OPIA (1,1)
Consider Eq. (4.1) as:
OPIA (1,1) requires to compute:
One may start the iteration by taking a trivial solution which satisfies the given initial conditions:
Substituting (4.5) into Eq. (4.4), we have
Now, Eq. (4.6) is inserted into Eq. (3.2) and applying the initial conditions we get
It is worth mentioning that
does not represent the first correction term; rather it is the approximate solution after the first iteration. Following the same procedure, we obtain new and more approximate results:
To determine the constants, we proceed as in Section 3. First, the residual
Inserting the constants into Eq. (4.9), we obtain the approximate solution of the third order:
Note that some complex numbers arise from solving Eq. (4.10). They can also be used instead of to get the same result. We here give only real solutions for simplicity.
4.2 OPIA (1,2)
One can construct the OPIA (1,2) by taking one correction term in the perturbation expansion and two derivatives in the Taylor series. Note that one needs to enter the data in Eq. (2.4) into the computer for PIA (1,2). But, it is sufficient to use
Using the trivial solution
, we have second order problem
Using Eqs. (3.2), (4.15) and the initial conditions, we obtain
Following the same procedure using (4.16), the second iteration is obtained as
One can easily realize that, we have functional expansion for OPIA (1,2) instead of a polynomial expansion.
Following the same procedure, from the residual
Thus, we have the second-order approximate solution:
One can also compute more approximate results by following the same procedure with a computer program. We do not give higher iterations due to huge amount of calculations. Fig. 1 and Table 1 shows a comparison of OPIAs and exact solution. It is clear that the results obtained by OPIM are more accurate than those of PIM in Aksoy and Pakdemirli (2010).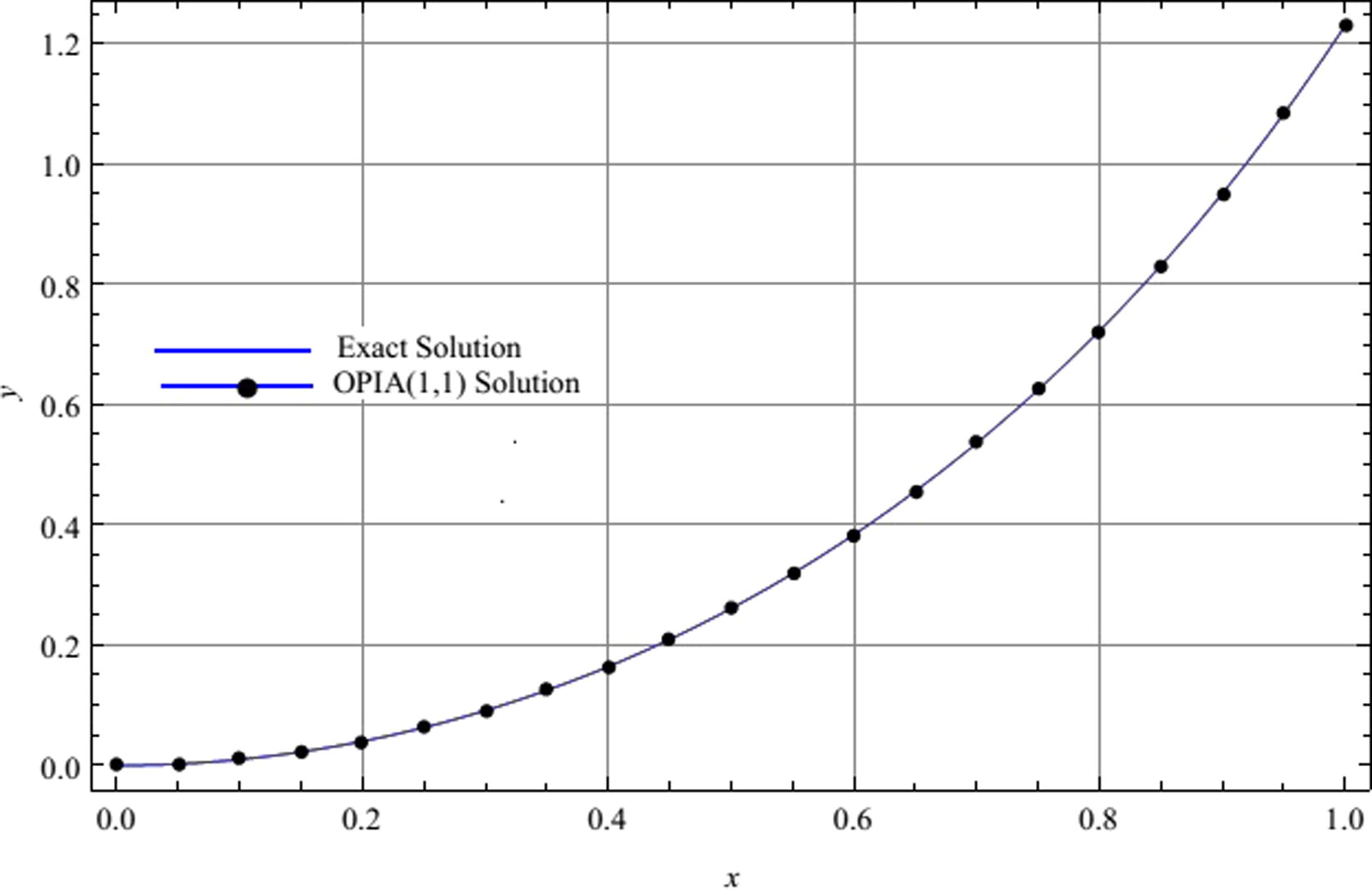
Comparison between the three-term OPIA (1,1) approximate solution and the exact solution for Example 1.
x
Absolute errors for OPIA (1,1) solutions
Absolute errors for OPIA (1,2) solutions
Exact solution
0.1
0.000449452
0.000169553
0.010016711
0.2
0.001595127
0.000583911
0.040269546
0.3
0.002812140
0.000976872
0.091383311
0.4
0.003000543
0.000963454
0.164458038
0.5
0.000485555
0.000139394
0.000126132
0.261168480
0.6
0.007148548
0.001752633
0.000116507
0.383930338
0.7
0.023329621
0.004551758
0.000144037
0.000354849
0.536171515
0.8
0.052947212
0.007229526
0.000727717
0.000982654
0.000128213
0.722781493
0.9
0.103126097
0.007116353
0.001202366
0.002323371
0.000452361
0.950884887
1
0.184637089
0.001509956
0.000365479
0.005024005
1.231252940
Example 2. Bratu’s first boundary value problem is given as (Wazwaz, 2005):
4.3 OPIA (1,1)
An artificial perturbation parameter is inserted for Eq. (4.21) as follows
By making necessary computations using Eqs. (2.2), (4.3) and setting
, we easily get
One may start with the trivial solution
For the constants
and
, the method given in Section 3.(d) is used, and we obtain the following values for
:
4.4 OPIA (1,2):
One just needs to construct
After making the relevant calculations, the algorithm takes the simplified form:
Using Eqs. (3.2), (4.24), (4.32) and the initial conditions, we obtain
For the constants
and
in Eq. (4.34), we proceed as earlier and get
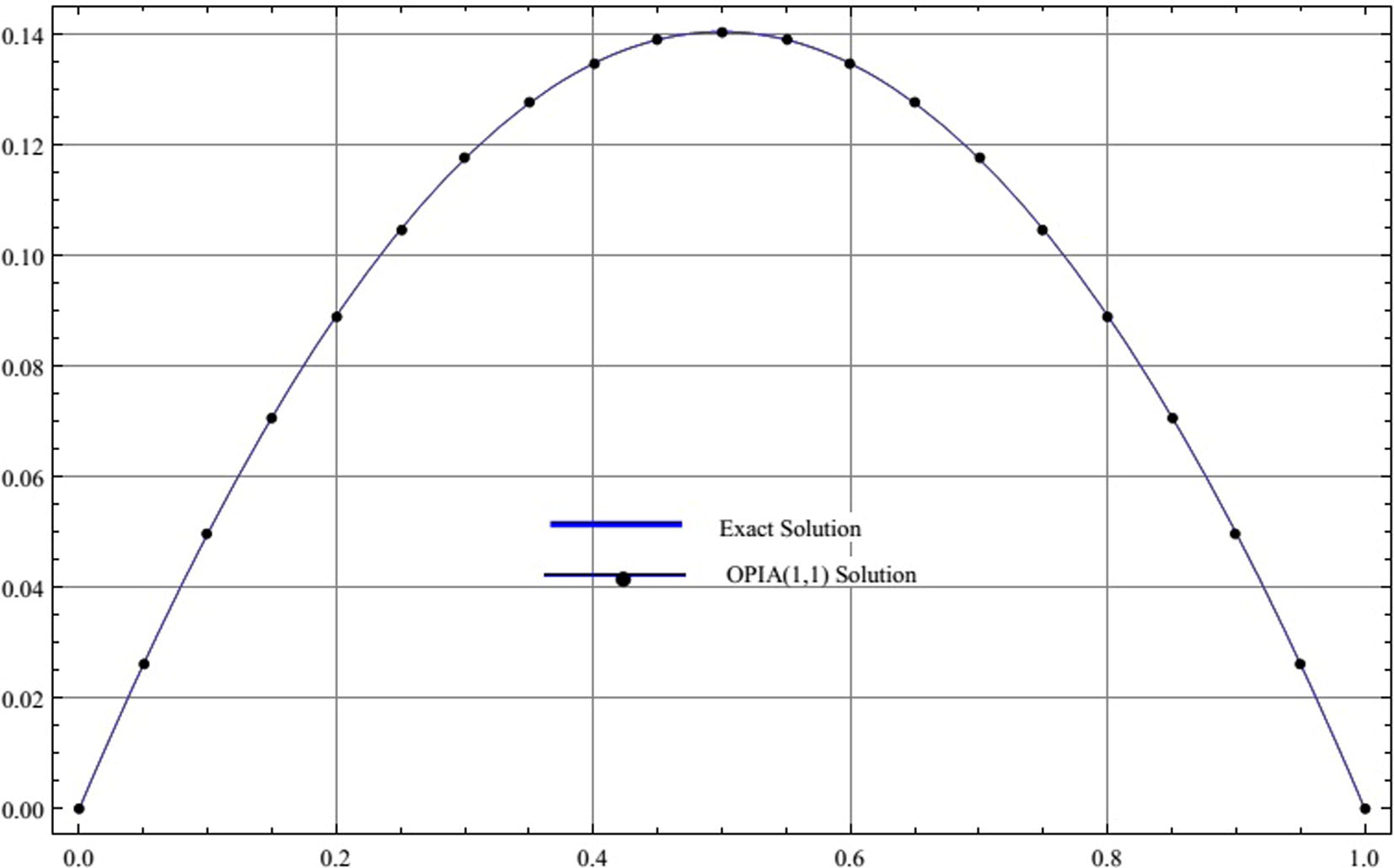
Comparison between the three-term OPIA (1,1) approximate solution and the exact solution for Example 2.
x
Absolute errors for OPIA (1,1) solutions
Absolute errors for OPIA (1,2) solutions
Exact solution
for
0.1
0.0498465
0.2
7.5067
0.0891894
0.3
0.1176084
0.4
0.1347894
0.5
0.1405383
0.6
0.000121368
0.1347894
0.7
0.000802364
0.1176084
0.8
0.000110879
0.0891894
0.9
0.000569203
0.0498465
Example 3. Consider Bratu’s second boundary value problem (Wazwaz, 2005)
Exact solution of this problem is mistakenly given as
4.5 OPIA (1,1)
By rearranging Eq. (4.37) as
Without going into details here, we just give the successive iterations:
Proceeding as earlier we find constants
and
:
Inserting the constants into Eq. (4.45), we obtain the approximate solution of the third order:
4.6 OPIA (1,2)
After making the relevant calculations, the algorithm
Using Eqs. (3.2), (4.49) and the initial conditions, we get
By using the above values, the approximate solution of the second order is:
One can easily observe from Table 3 and Fig. 3 that the results agree very well with the exact solution.
x
Absolute errors for OPIA (1,1) solutions
Absolute errors for OPIA (1,2) solutions
Exact solution
0.1
0.0000752784
0.0000608251
0.0000719575
0.269276469
0.2
0.0004108547
0.0001009657
0.0000183205
0.462340122
0.3
0.0000296314
0.0000723684
0.592783600
0.4
0.0000955682
0.0000135841
0.668371029
0.5
0.0002856413
0.693147180
0.6
0.0000213685
0.668371029
0.7
0.0000723646
0.592783600
0.8
0.0000108799
0.462340122
0.9
0.0005692033
0.000111947
0.0000523313
0.269276469
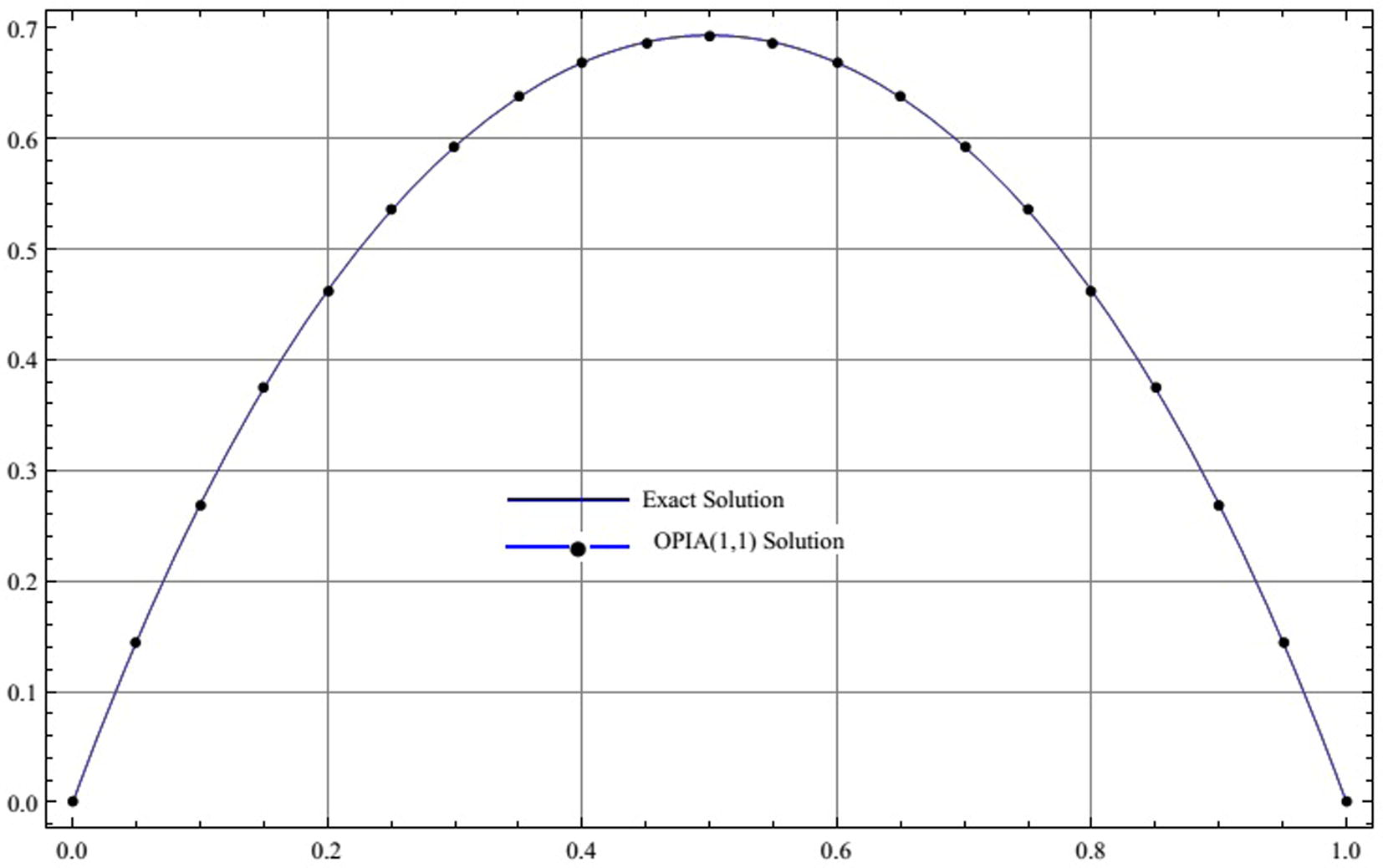
Comparison between the three-term OPIA (1,1) approximate solution and the exact solution for Example 3.
5 Conclusions
In this paper, a new technique OPIM is employed for the first time to obtain a new analytic approximate solution of Bratu-type differential equations. This new method provides us with an easy way to optimally control and adjust the convergence solution series. OPIM gives a very good approximation even in a few terms which converges to the exact solution. This fact is obvious from the use of the auxiliary function which depends on n coefficients . The results obtained in this paper confirm that the OPIM is a powerful and efficient technique for finding nearly exact solutions for differential equations which have great significance in many different fields of science and engineering.
References
- A review of the decomposition method in applied mathematics. J. Math. Anal. Appl.. 1988;135(2):501-544.
- [Google Scholar]
- New perturbation–iteration solutions for Bratu-type equations. Comput. Math. Appl.. 2010;59(8):2802-2808.
- [Google Scholar]
- New perturbation–iteration solutions for nonlinear heat transfer equations. Int. J. Numer. Methods Heat Fluid Flow. 2012;22(7):814-828.
- [Google Scholar]
- Numerical solution of Bratu-type equations by the variational iteration method. Hacettepe J. Math. Stat.. 2010;39(1)
- [Google Scholar]
- Comparison of solutions of systems of delay differential equations using taylor collocation method, Lambert W function and variational iteration method. Sci. Iran. Trans. D, Comput. Sci. Eng. Electr.. 2015;22(3):1052.
- [Google Scholar]
- The use of variational iteration method, differential transform method and Adomian decomposition method for solving different types of nonlinear partial differential equations. Int. J. Nonlinear Sci. Numer. Simul.. 2006;7(1):65-70.
- [Google Scholar]
- Comparison of Adomian decomposition method and Taylor matrix method in solving different kinds of partial differential equations. Int. J. Model. Optim.. 2014;4(4):292.
- [Google Scholar]
- Efficient Jacobi-gauss collocation method for solving initial value problems of Bratu type. Comput. Math. Math. Phys.. 2013;53(9):1292-1302.
- [Google Scholar]
- Variational approach to the Lane–Emden equation. Appl. Math. Comput.. 2003;143(2):539-541.
- [Google Scholar]
- Variational iteration method for Bratu-like equation arising in electrospinning. Carbohydrate Polym.. 2014;105:229-230.
- [Google Scholar]
- An analytical approach to non-linear dynamical model of a permanent magnet synchronous generator. Wind Energy. 2015;18(9):1657-1670.
- [Google Scholar]
- Application of the optimal homotopy asymptotic method to squeezing flow. Comput. Math. Appl.. 2010;59(12):3858-3866.
- [Google Scholar]
- Solving polluted lakes system by using perturbation-iteration method. Int. J. Comput. Appl.. 2015;114(4)
- [Google Scholar]
- Optimal homotopy analysis method. In: Homotopy Anal. Method Nonlinear Differ. Equ.. Springer; 2012. p. :95-129.
- [Google Scholar]
- Application of optimal homotopy asymptotic method for solving nonlinear equations arising in heat transfer. Int. Commun. Heat Mass Transfer. 2008;35(6):710-715.
- [Google Scholar]
- Optimal parametric iteration method for solving multispecies Lotka-Volterra equations. Discr. Dyn. Nat. Soc. 2012
- [Google Scholar]
- He’s homotopy perturbation method for solving heat-like and wave-like equations with variable coefficients. Phys. Lett. A. 2008;372(38):5944-5950.
- [Google Scholar]
- Solution of the one-dimensional Bratu equation arising in the fuel ignition model using ann optimised with PSO and SQP. Connection Sci.. 2014;26(3):195-214.
- [Google Scholar]
- Perturbation–iteration method for first-order differential equations and systems. In: Abstract and Applied Analysis. Vol vol. 2013. Hindawi Publishing Corporation; 2013.
- [Google Scholar]
- New perturbation iteration solutions for Fredholm and Volterra integral equations. J. Appl. Math. 2013
- [Google Scholar]
- Adomian decomposition method for a reliable treatment of the Bratu-type equations. Appl. Math. Comput.. 2005;166(3):652-663.
- [Google Scholar]







