Fragmented protein sequence alignment using two-layer particle swarm optimization (FTLPSO)

1 Introduction

Bioinformatics is an interdisciplinary field which studies combining aspects of biology, mathematics, and computer science. The bioinformatics can develop and improve methods for storing, retrieving, organizing and analyzing biological data (Cohen, 2004). A major activity in bioinformatics is to develop software tools to generate useful biological knowledge. One of the very important areas in bioinformatics is sequence alignment. The first step of creating phylogenetic trees is comparing sequences, grouping them according to their degree of similarity using alignment. Determination of the consensus sequence of several aligned sequences can help develop a finger print sequence which allows the identification of members of distantly related protein family. Most recent protein secondary structure prediction and analysis methods also use sequence alignments to improve the prediction quality (Di Francesco et al., 1996; Jagadamba et al., 2011).

Sequence alignment is used to arrange the sequences of DNA, RNA, or protein to identify regions of similarity. When regions of similarities between aligned sequences increase, it gives information that there is a similarity between these sequences in their function, their secondary and tertiary structure (Cohen, 2004). Solving the sequence alignment problem depends on gap insertion (Katoh and Standley, 2016). The gap should be inserted in correct places such that the alignment can achieve high residue matching and high scores Alignment problem may be applied on only two sequences, called pairwise alignment, PWA (Agrawal and Huang, 2009; Sierk et al., 2010), or on more than two sequences, called multiple sequence alignment, MSA (Sievers et al., 2011; Subramanian et al., 2008).

The optimization problem of the MSA is used to be solved using dynamic programming (Needleman and Wunsch, 1970; Smith and Waterman, 1981), and progressive methods (Al Ait et al., 2013; Lalwani et al., 2015). However, problems of high processing and high memory usage may be faced with no guarantee that the system will reach the optimal solution. The new trend is using iterative approach techniques due to their simplicity, and ability to solve multidimensional optimization problems in many fields (Das et al., 2008; Kiranyaz et al., 2009). Particle swarm optimization (PSO) is a swarm intelligent technique which proves its ability in solving MSA problem. However, the PSO suffers from the trapping of particles in local optima. Moreover, the PSO algorithm can handle short sequences in an efficient way, but increasing sequence lengths lead to decreasing solution accuracy. The main targets of this paper are to:

• –

  Pave the way for PSO to deal with different sequence lengths.

• –

  Give PSO the ability to solve MSA problems and achieve high scores.

• –

  Make PSO safe from falling in a local optimal point as possible.

To achieve these goals, fragmentation is proposed to shorten the long sequences, and to let the swarm focus on finding the optimal solution of the small fragment within a small search space, which has a less number of local optimal solutions. Then, a PSO variant is selected to align each fragment alone. This variant is two-layer PSO (TLPSO). It is selected due to its ability to solve unconstrained problems such as MSA. These two layers contain many swarms: R swarms in the first layer, and one swarm in the second layer. Particles in every swarm are dealing with each other using Local-PSO variant as a way to give the particles more ability to reach the optimal solution without trapping in a local optima. Finally, mutation is used to give more help to the swarm if it has been trapped.

The rest of paper is organized as follows: the history of alignment problem is mentioned in Section 2, followed by the alignment scoring functions in Section 3. A description of particle swarm optimization technique is illustrated in Section 4. The proposed algorithm is introduced in Section 5. Finally, the computed results with discussion, followed by some parametric studies are presented in Section 6.

2 Related work

Many methods are presented to solve alignment method such as dynamic programming, progressive, consistency-based, and iterative methods.

Dynamic programming technique creates a matrix of $n$ -dimensions for n sequences. The matrix is filled with scores by some calculations, and then the optimal path can be found. The dynamic programming technique gives an optimal alignment score, but it depends on the number of sequences n. Therefore, the computational time and memory usage will be increased by increasing the $n$ value. So, dynamic programming can’t be used for more than two sequences practically although it can align multiple sequences theoretically (Suresh and Vijayalakshmi, 2013).

Progressive alignment is used to align multiple sequences, by aligning each two sequences together, creating a guide tree based on the similarity score of each two pairs, and aligning all sequences one by one. One of the first and most famous progressive alignment methods is CLUSTAL W (Thompson et al., 1994). One disadvantage of a progressive alignment is that the algorithm is greedy. This means that the alignment depends on the early aligned pair of sequences. Therefore, any early happened mistake will affect the rest of the progressive alignments. Also the time to perform such progressive alignments is proportional to the number of sequences (Lalwani et al., 2013b). To overcome the greedy problem, CLUSTAL W2 (Larkin et al., 2007) does a progressive alignment many times using different gap penalty scores, and accepts the best score. KALIGN (Lassmann and Sonnhammer, 2005) also follows the standard progressive alignment except it depends on Wu–Manber (Wu and Manber, 1992) as a pairwise distance estimator instead of $k$ -tuple used by CLUSTAL.

Another approach is a consistency based approach, which depends on the principle of maximizing the agreement of pairwise alignment. It looks for an agreement in which the created tree gives high accuracy when used for further progressive alignment. DIALIGN (Morgenstern et al., 1996), and TCOFFEE (Notredame et al., 2000) are two examples of consistency based algorithm. DIALIGN combines local and global alignment features. It depends on discovering local homologies among sequences, as discovering conserved (functional) regions. Many variants of DIALIGN are presented including Anchored DIALIGN (Morgenstern et al., 2006) and DIALIGN-TX (Subramanian et al., 2008). The newest variant depends on PFAM database (Finn et al., 2008) which collects protein families, in which these families are represented by multiple sequence alignment. This variant is called DIALIGN-PFAM (Al Ait et al., 2013). TCOFFEE depends on creating libraries of both global and local pairwise alignment as a step to do multiple sequence alignment.

Because dependency on consistency based approach alone does not guarantee the accuracy of the alignment, post processing using iterative refinement is used to improve the performance of progressive alignment. MAFFT (Katoh et al., 2002), and MUSCLE (Edgar, 2004) are two examples of progressive-iterative approach. Every iteration they update the tree and re-do MSA until there is no improvement in the score. Computational intelligence techniques also used to enhance the alignment results given by progressive alignment techniques (Pankaj and Pankaj, 2013; Suresh and Vijayalakshmi, 2013). Other approach is probabilistic consistency transformation based strategy (using HMM), which is used from many tools such as probcon (Do et al., 2005), probalign (Roshan and Livesay, 2006), and CLUSTAL Omega (Sievers et al., 2011). This approach is used to decide the probability of distribution for every pairwise alignment done on the whole sequences of the database before the creation of the tree.

While probabilistic consistency, and progressive-iterative refinement approaches give accurate results, their computations are complex (Mount, 2004), and their memory usage is high (Pais et al., 2014). On the other hand, iterative approach based computational intelligence techniques overcome progressive approach, which gives equality in priority to all sequences. Therefore, accurate alignment results can be achieved using simple computations (Arulmani et al., 2012; Lalwani et al., 2013b). Many papers tried to solve the problem using iterative approach only, like simulated annealing (Kim et al., 1994), Genetic algorithm (Botta and Negro, 2010; Notredame and Higgins, 1996), and particle swarm optimization (Xu and Chen, 2009; Long et al., 2009a, 2009b; Lalwani et al., 2013b; Lalwani et al., 2015).

Simulated annealing was too slow but it works well as an alignment improver. For small numbers of sequences, genetic algorithm (GA) is a better alternative for finding the optimal solution. However, as the number of sequences increases, it can fall behind optimal solutions and exponential growth in time may be observed. PSO proves its superiority in speed convergence than simulated annealing, and its ability to align number of sequences larger than genetic algorithm. In addition, PSO has a few numbers of parameters that need tuning and parameter setting (Lalwani et al., 2013a). Standard PSO performance in short sequences is better than long ones (Xu and Chen, 2009; Long et al., 2009a; Long et al., 2009b). Then, TLPSO with mutation is proposed for the first time by Chen (2011), and tested on nine optimization problems, and proves its ability to get the optimum solution. For MSA, TLPSO (Lalwani et al., 2015) is tested with creation of new swarm every iteration, as a way for mutation, and proves its superiority than standard PSO. However, more enhancements on PSO are still needed to reach the optimal solution especially for long sequences.

In this paper, the FTLPSO is proposed. A fragmentation technique based on $k$ -tuple is applied to shorten the long sequences to small sub-sequences, aiming to solve the problems of PSO. Then, TLPSO is applied as a suitable variant for MSA problem.

3 Scoring functions for MSA

The performance of the alignment process is measured by scoring functions which reflect the accuracy of the alignment. The most used two scoring functions are:

• -

  Column Score (CS) score is used to increase the number of matched columns:

For the aligned dataset of $n$ sequences, and alignment length AL, the scoring function is calculated for every column of position $x$ as:

• –

  Sum of Pair (SOP) score is applied to increase the similarity match between every two sequences:

For an aligned dataset of $n$ sequences, the scoring function is calculated for every two sequences $S_i\text{,}{S}_j$ as shown in Eq. (2):

The alignment aims to increase the number of residue matches and decrease the number of mismatches. In the previous equation, two residues at position $x$ of sequences $i\text{,}j$ are compared. If they are similar, a score of value $(A)$ is added as a reward. However, if there is a mismatch between these two residues or if a residue is matched with a gap, a penalty $(B\mathit{or}C)$ is subtracted as negative score, respectively. PAM and BLOSUM are the most famous scoring matrices to give the match and mismatch scores for protein sequence alignment. The most widely used gap penalty function is the affine gap penalty (Gotoh, 1983). In the affine gap penalty model, a gap series of length $\ell$ is given two weights. The first weight is related to the first gap, which is the gap open penalty go. The other weight $\mathit{ge}$ is the weight to extend the gap with one more space. The total penalty for a series of gaps of length $\ell$ is:

4 Particle swarm optimization

Kennedy and Eberhart (1995) first introduced particle swarm optimization (PSO) in 1995. It mimics the social behaviour of bird flocks or fish schools. Every time, each particle in the swarm flies to its next position with a specific speed depending on its achieved best position, and the global best position reached by any particle in the swarm. The update rule of particle positions every iteration can be seen in the next two equations as follows:

• $t$ is the iteration number, ranges from (1: $t_{\mathit{max}}$ ).

• $m$ is the particle number, ranges from (1: M).

• $d$ is the dimension number, ranges from (1: D).

• $r1\text{,}r2$ are random numbers between (0, 1).

• $c1\text{,}c2$ are positive values called cognitive acceleration coefficient, and social acceleration coefficient respectively.

• w is called inertia weight, introduced to accelerate the convergence speed of the PSO, takes values between [0, 1].

• $x$ is the matrix of size (M, D) where M is swarm size, and D is the number of dimensions, to store the current positions of each dimension of all particles.

• $v$ is a matrix of the same size of $x$ , which gives the change rate of positions (velocity) of each dimension d for every particle $m$ .

• $\mathit{pbest}$ (Particle best) is also a matrix of the same size of $x$ to store the best positions every particle reached from iteration (1: $t-1$ ):

  (7)
  $${\mathit{pbest}}_{\mathit{md}}=\text{max}[\mathit{score}(x_{\mathit{md}}^1):\text{score}(x_{\mathit{md}}^{t-1})]$$

• $\mathit{gbest}$ (Global best) of size (1, D) stores the pest N- dimensional positions which gives the best score by any particle from iterations (1: $t-1$ )

  (8)
  $${\mathit{gbest}}_d=\text{max}[\mathit{score}({\mathit{pbest}}_{\mathit{md}})]$$

5 Proposed method FTLPSO

The proposed algorithm is divided into two main steps:

1. Fragmentation process, to shorten the longest sequences, and Pave the way for PSO. In this paper, a $k$ -tuple method is selected as a fragmentation technique. By the end of fragmentation process, an index table for fragment position is created.

2. PSO algorithm, to perform the alignment process on fragments. Two layers of swarms are created, as the swarms in each layer will focus on one of the two scoring functions of the MSA to appraise their performance. In each swarm, local-PSO is used as a good solution to achieve divergence. Also a mutation is applied on the best particle every iteration to reduce the risk of falling in a local optima.

5.1

5.1 Fragmentation: table of $k$ -tuples

It is worth noting that PSO is performing well with short sequences (Xu and Chen, 2009; Long et al., 2009a, 2009b). A fragmentation technique is used to shorten the sequences of the datasets. Additionally, if one fragment is mis-aligned, this will not affect the other fragments. Fragmentation depends on searching for conserved regions (also called motifs or blocks) and aligning them, and then aligning the regions between these blocks to make a complete alignment. The fragmentation technique used here is $k$ -tuple. Fragmentation based on k-tuple or $k$ -word searches for a word of length k. This technique is previously used in one of the oldest and fastest pairwise alignment methods: FASTA (Lipman and Pearson, 1985). Due to its simplicity and speed, the $k$ -tuple could be enough in molecular phylogeny and taxonomy without the need for alignment in the future (Zuo et al., 2014). As the word length (the $k$ value) increases, the accuracy of the match between the two words also increases. The $k$ -tuple can also have a number of mismatches that don’t exceed a value Δ (Fig. 1), where Δ mutations give non-negative score in the substitution matrix. In this case, these characters are not matched but they have a degree of similarity in their chemical structure. This -tuple technique with mutations is called Wu–Manber (Wu and Manber, 1992).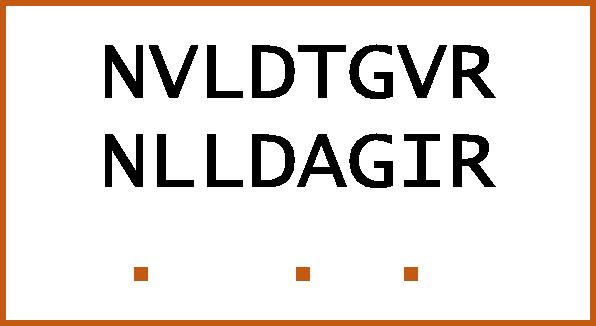

Close

Figure 1

Match of two words of word length $k$  = 8 and Δ = 3 mutations. Depending on pam250 matrix, score (V, L) = +2, score (T, A) = +1, and score (V, I) = +4.

Export to PPT

To find a word of length $k$ in the dataset of $n$ sequences, one of these $n$ sequences is assumed to be a query. Every $k$ -tuple of the query sequence is scanned with all the $n-1$ left sequences. If this word is found in all sequences, the positions of this word in all sequences are inserted into a table. This step is repeated for (L − k + 1) $k$ -tuples for the query of length L.

After the table has been created, and an overall check has been done to make sure that there is no conflict, two more rows must be added. As illustrated in the example in Fig. 2, all matched words of $k=3$ and $\mathrm{\Delta }=0$ are gathered in table T1. The first and the last columns are added, which contain the index of the first, and the last character in every sequence as shown in table T2. The aim of this table is to find the $k$ -tuple words and connect between $k$ -tuple search method and PSO. The PSO will take every two successive rows and deal with the segments in-between. Adding the first and the last two in the table will let PSO deal with the first and the last two fragments. Every time, PSO will deal with one fragment. To get the boundaries of the $i$ th fragment for the $j$ th sequence, every two successive rows $(i\text{,}i+1)$ in the table T2 should be considered following the equation:

(9)

$$\mathit{Boundary}(j\text{,}i)=[\mathit{table}(i\text{,}j)+\mathit{table}(i\text{,}n+1)]:[\mathit{table}(i+1\text{,}j)-1]$$ where $\mathit{table}(i\text{,}n+1)$ indicates the $k$ -tuple length to let the PSO start taking the fragment after the $k$ -tuple ended. The aligned parts by the $k$ -tuple method are not included in the PSO calculation and may be misaligned if the particle is trapped in local optima.

Close

Figure 2

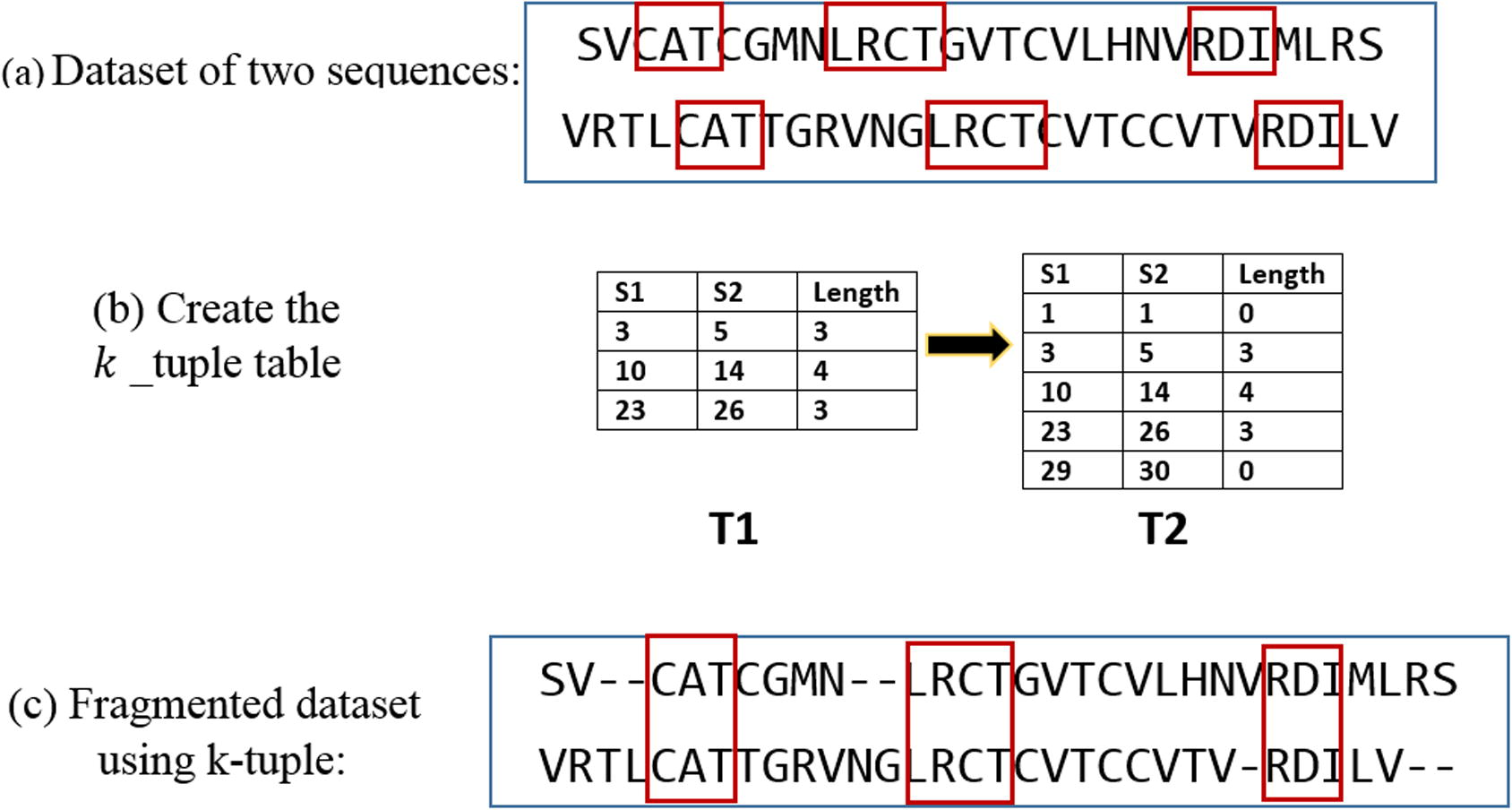
Example illustrates how the table linking between fragmentation and PSO is created.

Export to PPT

5.2

5.2 Alignment: PSO

5.2.1

5.2.1 Particle creation

In the alignment problem, we need to find the best location of gaps which will be added. So, particles here will carry the positions of these gaps in all sequences of the entered dataset. The number of dimensions for the particle will be equal to the number of gaps needed to be inserted to the sequences. Fig. 3 gives an example of a dataset of sequences filled with gaps.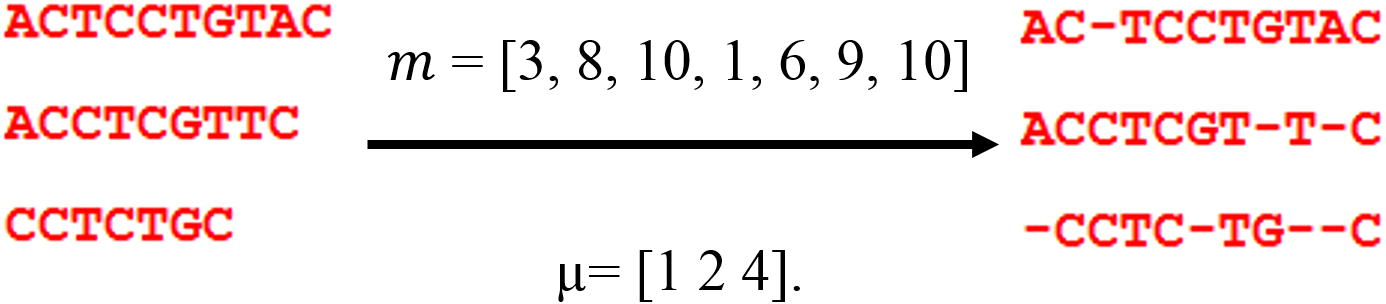

Close

Figure 3

Numerical example on how a particle of gap positions is created. m is a particle, and μ is a matrix helping the particle to decide to which sequence the gap belongs.

Export to PPT

In the example in Fig. 3, a particle $m$ here is represented as: m = [3, 8, 10, 1, 6, 9, 10] that carries the positions of gaps in the dataset. Another variable μ is needed here to show in which sequence in the dataset the gaps will be added. Simply, μ will carry a number of gaps that will be added in each sequence. To get the starting, and the ending positions of the gaps from the particle $m$ for sequence $j$ using matrix μ, next equations are used:

(10)

$${\mathit{pos}}_{\mathit{start}}(j)={\displaystyle \sum _{I=0}^{j-1}}\mu +1$$

(11)

$${\mathit{pos}}_{\mathit{end}}(j)={\displaystyle \sum _{I=0}^{j-1}}\mu +\mu (j)+1$$

And so, gaps will be added to sequence $j$ are:

(12)

$$\mathit{gaps}(j)=m({\mathit{pos}}_{\mathit{start}}:{\mathit{pos}}_{\mathit{end}})$$

The values of the gaps should be controlled by the length of the alignment (in Fig. 3), so $m$ matrix should contain values <11.

5.2.2

5.2.2 Local-PSO

The basic PSO discussed in the previous section is called global PSO, as all particles in the swarm follows only one particle, the one which gets the best score value. Dependency of all particles on only one particle in updating global best term causes fast convergence. If the $\mathit{gbest}$ is trapped, that mostly causes trapping of all other particles. One famous variant of PSO is local-PSO (Eberhart et al., 1996). Its main benefit over global-PSO is to keep the system divergent from trapping in local minima/maxima. Here, the swarm is divided into many sub-swarms, such that every particle calculates its local best value (instead of global best one) by finding the best positions of gaps which give the best score in the sub-swarm.

In local-PSO, every particle can choose its neighbours according to geographical area (or for alignment problem, it can selects particles of near scores), or randomly. In this paper, particles follow randomly chosen method. As illustrated in Fig. 4, random selection for neighbourhood can be only one time or every loop. The paper follows the selection of new neighbours every loop of DRN-PSO. It presents a form of dynamic random neighbourhood, which enables each particle to change its neighbourhood during searching for the optimal solution as shown in Fig. 5. This feature helps in increasing the swarm diversity (El-Hosseini et al., 2014). When the size of g $\mathit{best}$ matrix in Eq. (5) is equal to the size of one particle only, the size of $\mathit{lbest}$ here will be equal to the size of the swarm. That lets Eq. (5) transform to Eq. (13):

(13)

$$v_{\mathit{md}}^t=w^t.v_{\mathit{md}}^{t-1}+[c1.r1.({\mathit{pbest}}_{\mathit{md}}-x_{\mathit{md}}^{t-1})]+[c2.r2.({\mathit{lbest}}_{\mathit{md}}-x_{\mathit{md}}^{t-1})]$$

Close

Figure 4

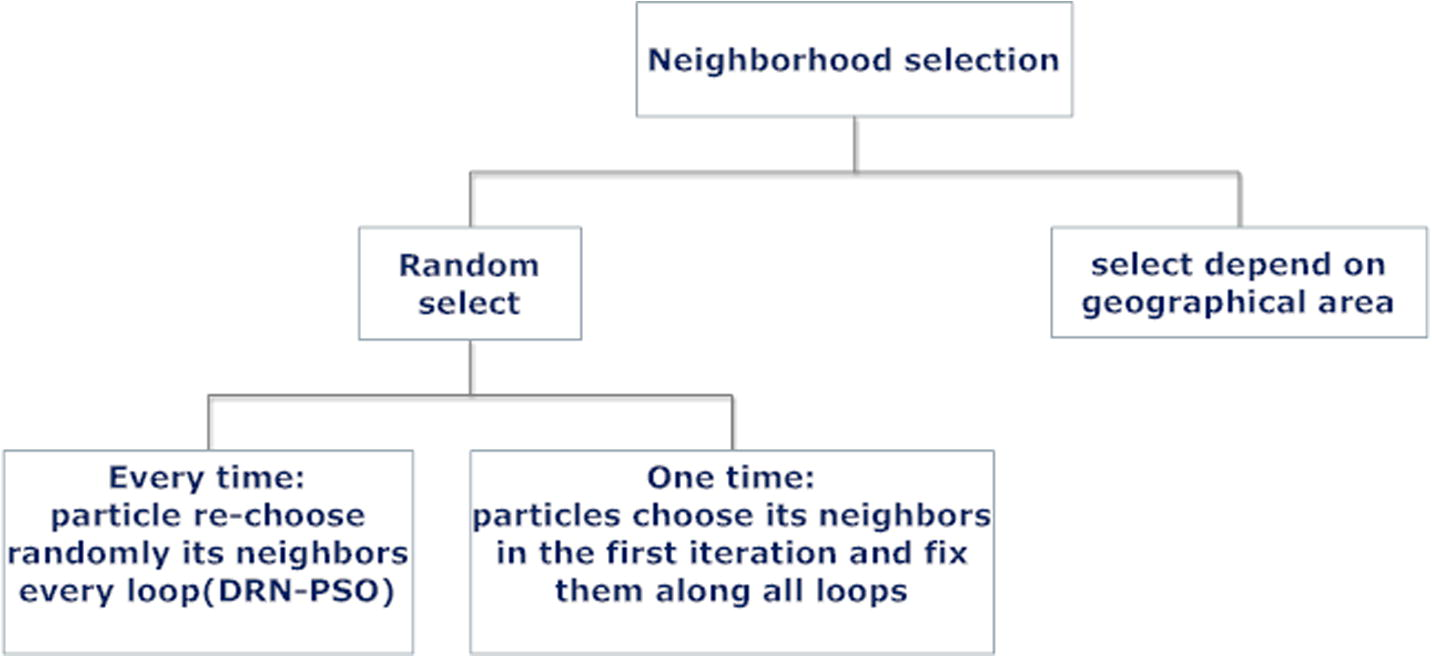
Simple classification for selecting neighbourhood in PSO.

Export to PPT

Close

Figure 5

DRN-PSO algorithm.

Export to PPT

5.2.3

5.2.3 Best particle mutation

Every iteration of the best particle mutation method, the best particle gbest is selected to be mutated. After mutation is done, the score is calculated and compared with the one before mutation. If the particle after mutation gives a higher score, then keep it and update the score value in the scoring matrix (Long et al., 2009b). The algorithm of the best particle mutation is illustrated in Fig. 6.

Close

Figure 6

Best particle mutation.

Export to PPT

5.2.4

5.2.4 Two-layer PSO (TLPSO)

TLPSO consists of two layers. The first layer contains R swarms as shown in Fig. 7, where all particles in one swarm are communicating with themselves, using a specified scoring function to get the optimal (or semi-optimal) solution for the problem. Every swarm in the first layer produces $\mathit{gbest}$ as an output, so for R swarm, we can get R gbest particles. These R particles will create the swarm in the second layer. Finally, one gbest particle (Gbest L2) will be resulted from the second layer.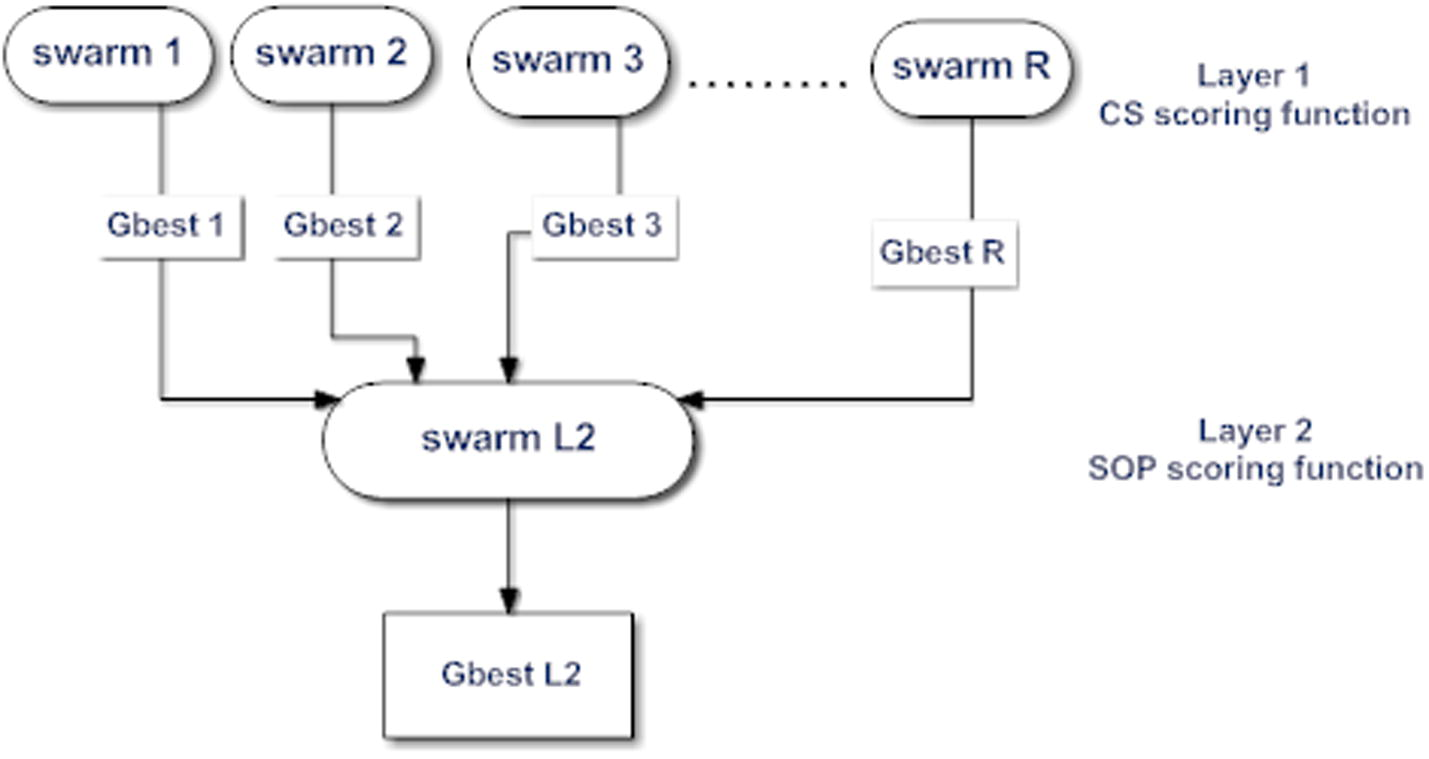

Close

Figure 7

TLPSO structure.

Export to PPT

All swarms in the first layer will use the CS scoring function mentioned in Eq. (1), and the swarm in the second layer will depend on the SOP scoring function mentioned in Eq. (2). The pseudo code for FTLPSO is shown in Fig. 8.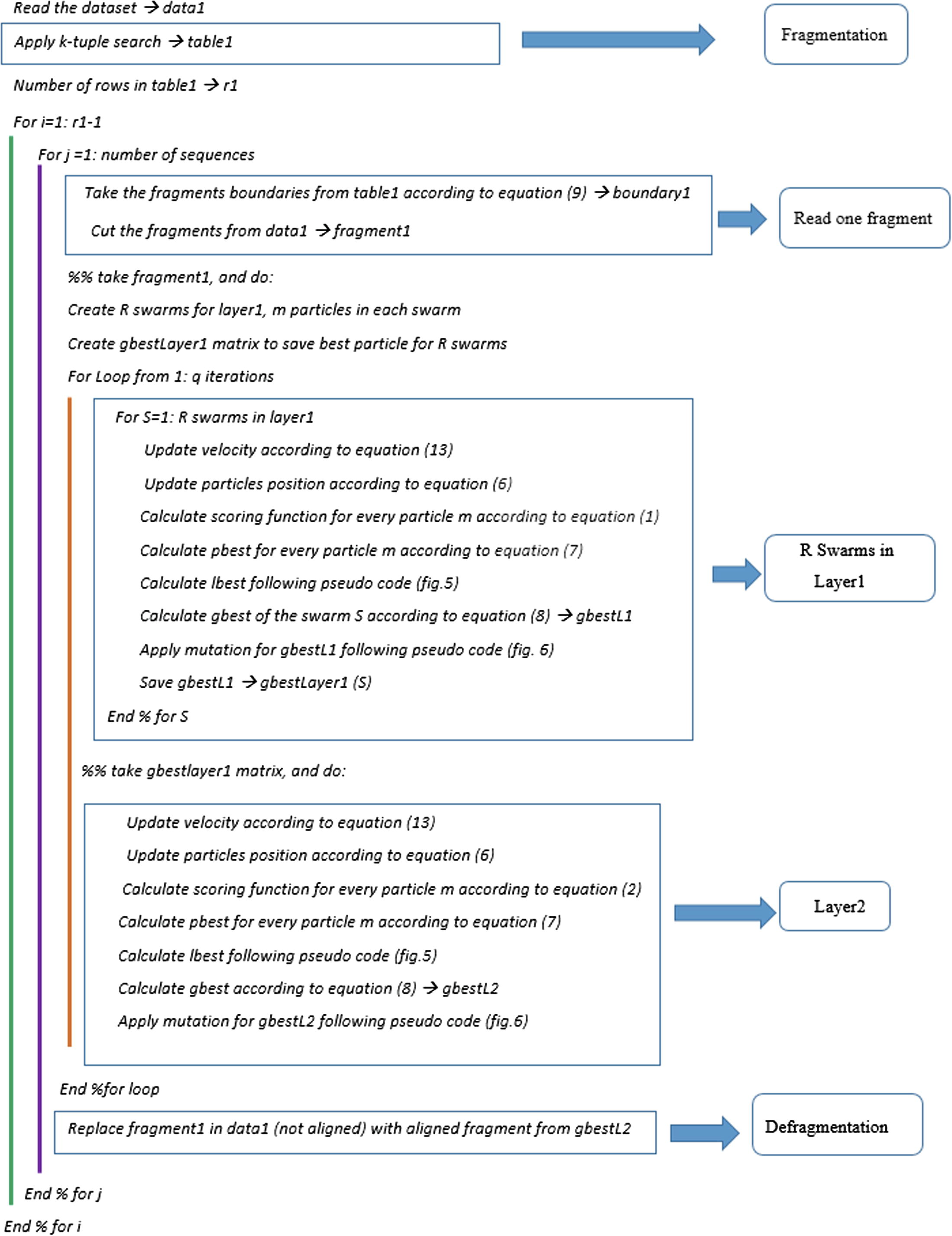

Close

Figure 8

FTLPSO code.

Export to PPT

6 Numerical results

According to the scoring functions: the scoring matrix used is PAM 250, and the gap penalty used is affine gap penalty with a gap open penalty $\mathit{go}$  = −10, gap extension penalty $\mathit{ge}$  = −0.3, and gap-gap penalty = 0. Concerning $k$ -tuple search: the value of $k$ is chosen to be =8, with maximum number of mutations Δ = 3, as a suitable selection for the tested datasets, which is not too long that the k-tuple method can’t find it, nor too short which causes conflicts (Lassmann and Sonnhammer, 2005).

According to the PSO: The number of neighbourhoods for local PSO = 3, and best particle mutation is considered in every iteration. The values of acceleration coefficients $c1$ and $c2$ are $c1=c2$  = 1.49618 (Eberhart and Shi, 2000). The velocity matrix $v$ is bounded between two values ( $v_{\mathit{min}}\text{,}{v}_{\mathit{max}}$ ) according to next equations:

Further, $w$ is exponentially decreased according to equation:

For two layers: number of swarms of the first layer R = 10, with 10 particles in each swarm, and the best 10 particles in layer1 will create the swarm in layer2.

The suggested algorithm has been implemented using MATLAB Ver. 8.2.0.701 (R2013b). The algorithm is applied on some Balibase (Bahr et al., 2001) benchmark datasets of different alignment lengths, and compared with five famous MSA tools: CLUSTAL Omega, CLUSTAL W2, TCOFFEE, KALIGN, and DIALIGN-PFAM (www.ebi.ac.uk; www.clustal.org; http://dialign-pfam). The comparative analysis with these tools is presented in Section 6.1. Next, Section 6.2 gives an answer for why the used parameters have been set as they are. The parameters of the velocity update equation (Eq. (13)), and sum of pair score (SOP) equation (Eq. (4)) are studied. In the numerical study for each parameter, only the value of the studied parameter is changed, and the others are kept fixed according to their values mentioned above.

6.1

6.1 Comparative analysis

Fig. 9 compares the results of standard PSO, TLPSO without fragmentation, and TLPSO with fragmentation (FTLPSO). The datasets are sorted according to their lengths. The figure represents that the standard PSO and the TLPSO have the ability to deal with short sequences. That appears in the first sequence (1fmb) where the SOP scores for standard PSO, TLPSO and FTLPSO are very close to each other. The standard PSO fails to do alignment for the rest of the datasets. TLPSO overcomes the standard PSO. However, it also gave poorer results, and failed to reach the optimal solution. FTLPSO succeeded to reach optimal (or semi-optimal) solutions, and overcome both standard PSO and TLPSO.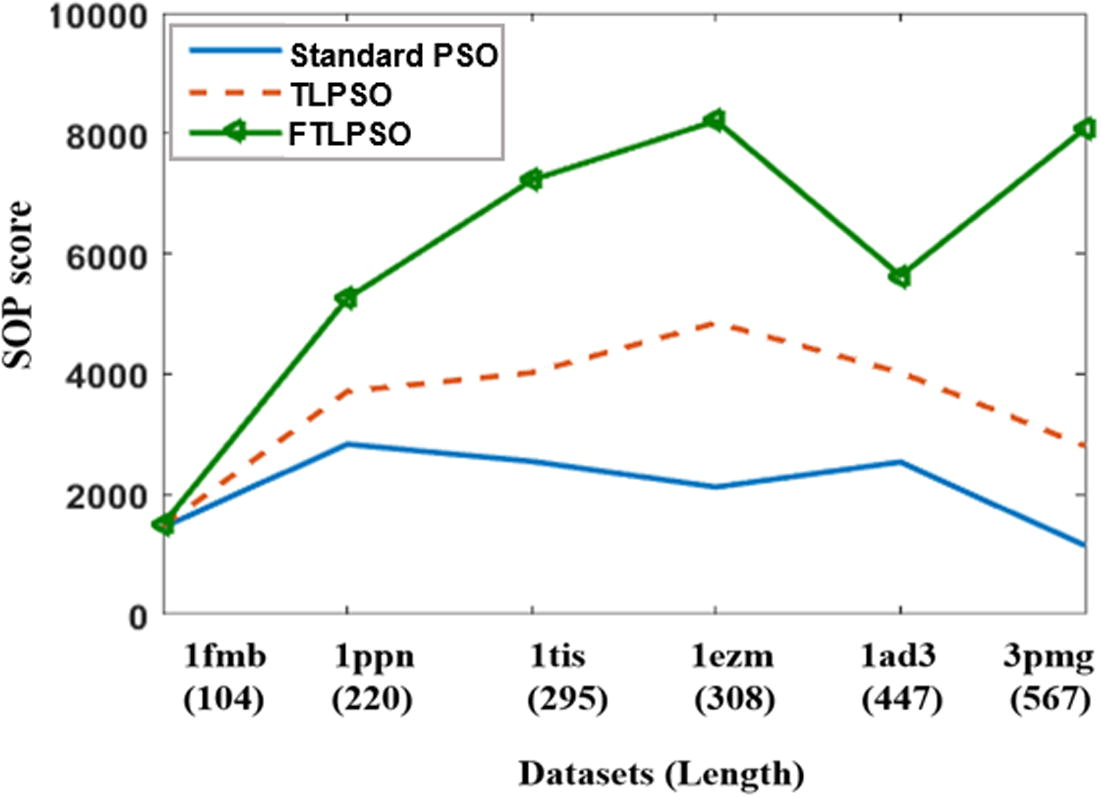

Close

Figure 9

Compare the results of standard, two layers before and after fragmentation (standard PSO vs TLPSO vs FTLPSO).

Export to PPT

Fig. 10 gives more details regarding the performance of standard PSO, and TLPSO for 3 datasets. For the shortest, and simplest dataset, 1fmb, Fig. 10a shows how the standard PSO reached a semi-optimal solution. However, TLPSO was able to reach the optimal solution, and with less numbers of iterations. With the increase in dataset length, and complexity, particles with 1ppn dataset tried to achieve good solution along 2000 iterations. TLPSO outperformed standard PSO. However, system couldn’t reach the optimal solution. It is worth to mention the role of best-particle mutation, which helps the system to move again after it has trapped in a local minima, as it is obvious at standard PSO in (Fig. 10b). 1tis suffered from an early trapping in local minima although TLPSO outrun standard PSO.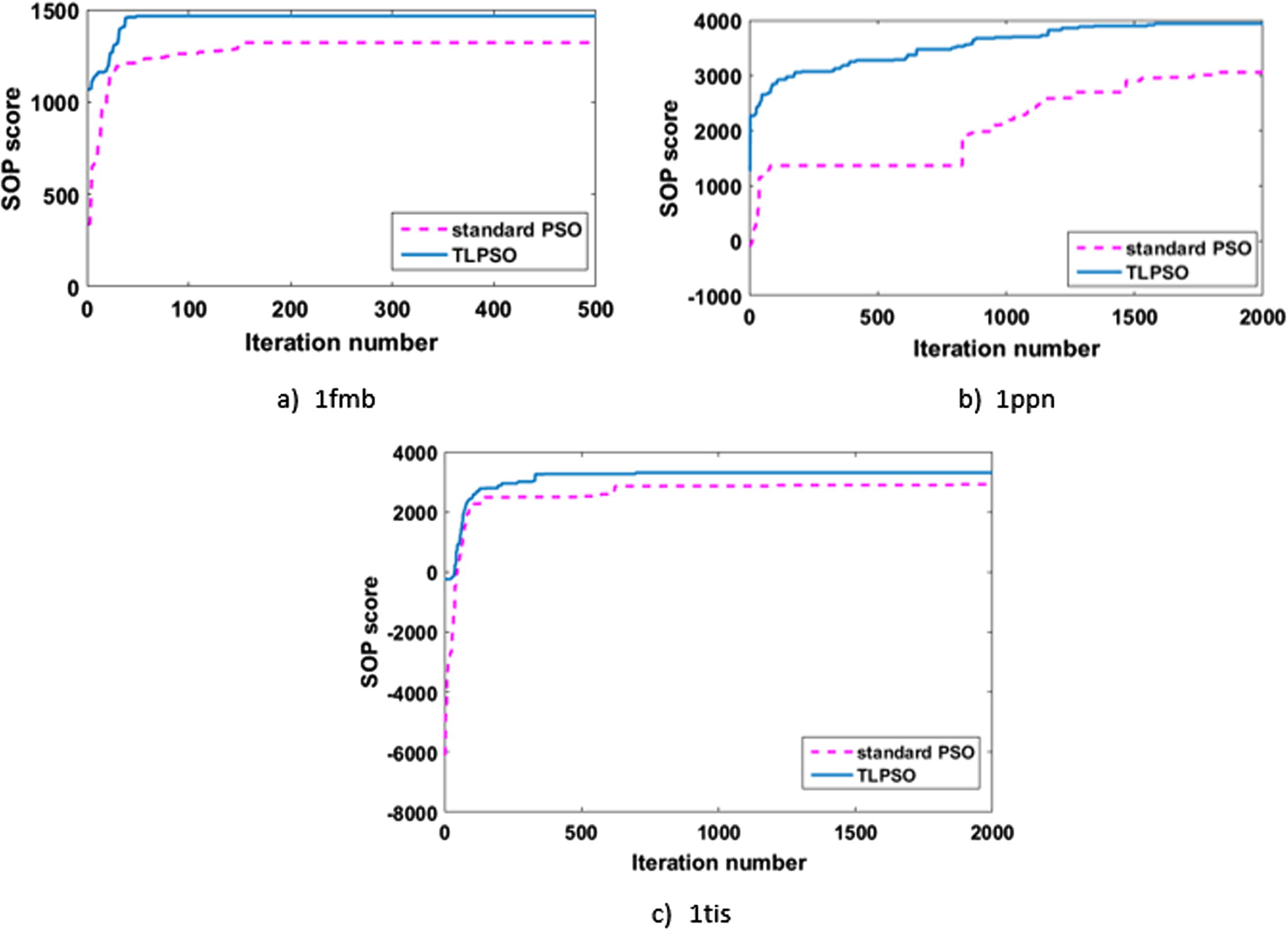

Close

Figure 10

Rate of convergence for standard PSO and TLPSO.

Export to PPT

The results in Table 1 shows the ability of the proposed method to align long sequences, and the PSO is not affected with the length of the datasets. That is clearly seen in (3pmg), the longest tested dataset, that the FTLPSO overcomes the other MSA tools. That proves that the FTLPSO is the best tool which tries to keep the scores high in all the tested datasets. But for the other tools, if they get a high score with one dataset, it may fall in the other. The average score for the tested datasets in Fig. 11 also shows the success of the proposed method. That is because:

• The fragmentation gives the ability to the swarm to search for the optimal solution within a smaller and bounded search space.

• One fragment will contain less number of local optimal points, which helps the particle to face less numbers of local optimal points.

• For each fragment, the swarm will concentrate on finding the optimal solution by dealing with less number of gaps, which should be added in this fragment.

• If the PSO can’t find the optimal solution in one fragment, the other fragments will not be affected, and the overall score will remain high.

Table 1 SOP score results for FTLPSO compared with other five MSA tools. The left column contains list of datasets, and the length of the longest sequence is mentioned in brackets. The highest score is in bold, and the second is underlined.

Dataset	Mean of 5 runs (FTLPSO)	CLUSTAL OMEGA	CLUSTAL W2	TCOFFEE	KALIGN	DIALIGN-PFAM
1fmb (104)	1495	1465.5	1453.5	1471.5	1465.5	1407.5
1ppn (220)	5256.1	5156.1	5170.9	5243.5	5230.9	5156.1
1tis (295)	7224.5	7225.1	7147.7	7156.8	7126.9	7100.5
1ezm (308)	8211.8	8102.9	8151 $\theta$	8141.7	8233.4	8119.7
1ad3 (447)	5632.7	5487.1	5603	5600.6	5681	5570.3
3pmg (567)	8079.8	7930.2	7955.9	8036.2	8032	7654.7
Mean	5982.85	5894.48	5913.67	5941.72	5961.6	5834.8

Close

Figure 11

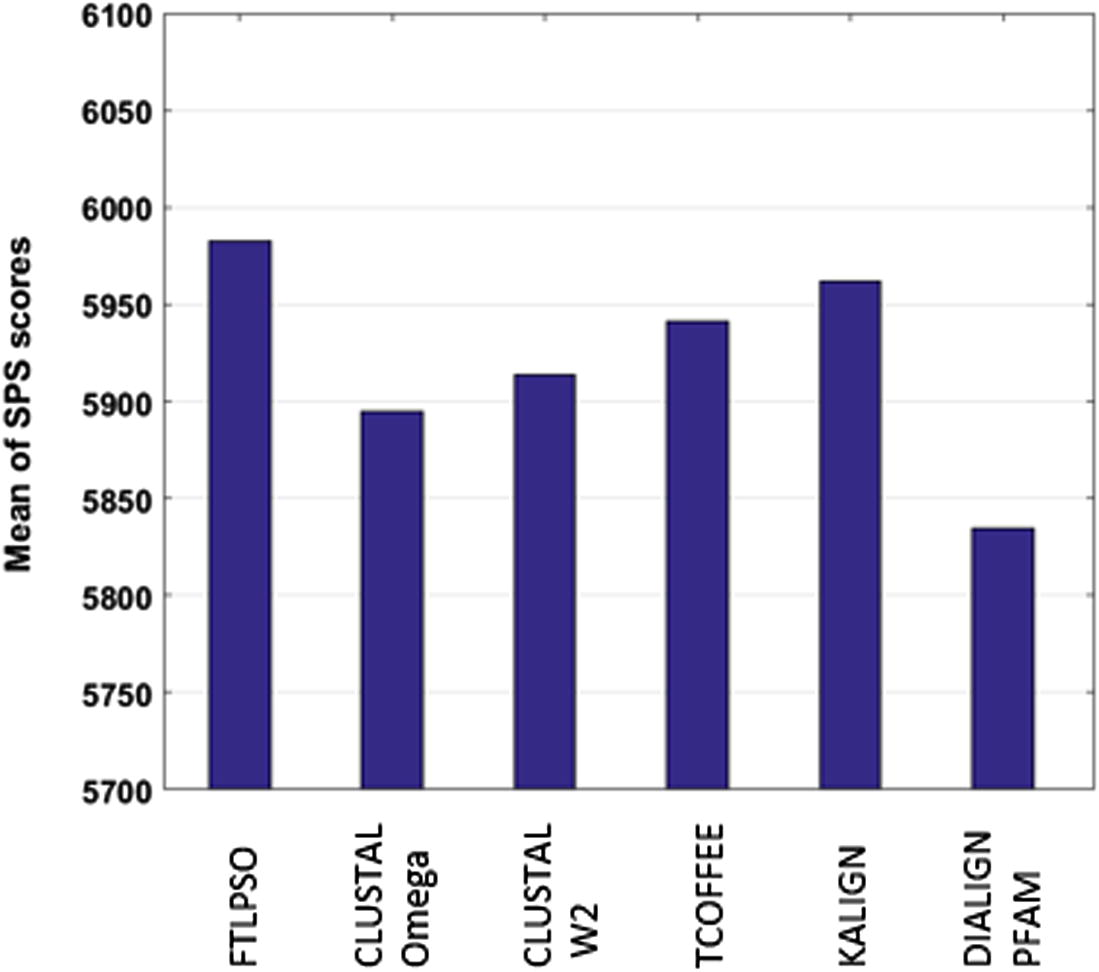
Mean of SPS scores for every MSA tool.

Export to PPT

Besides the role of fragmentation process, the high performance of PSO lies in:

• The PSO does not discriminate one sequence over another, and it is one of the most important benefits for PSO as an iterative tool, compared to other progressive tools.

• The cooperation between particles with each other’s to reach the optimal point of the highest score.

• Local PSO increases the swarm diversity, and lets the particles explore more points in the search space.

• Mutation which is applied on the $\mathit{gbest}$ particle also gives help if the $\mathit{gbest}$ has trapped in a local optima.

Figs. 12 and 13 give two examples to show the performance of the PSO on two fragments from 1ezm and 1ppn datasets. The selected fragment from 1ezm is of length 44, and 1ppn fragment is of length 104. For each fragment, every swarm in the first layer and the swarm in the second layer contain 10 particles, and each swarm runs for 100 iterations. For each fragment, the 10 swarms in the first layer run, and the CS score given by the best particle in layer 1 every iteration is presented in (12-a, 13-a). Figs. 12b and 13b show the progress of the swarm in the second layer. Rate of convergence for both layers have been normalized in (12-c, 13c) to show the effectiveness of the best particles from swarms in the first layer on the second layer’s swarm.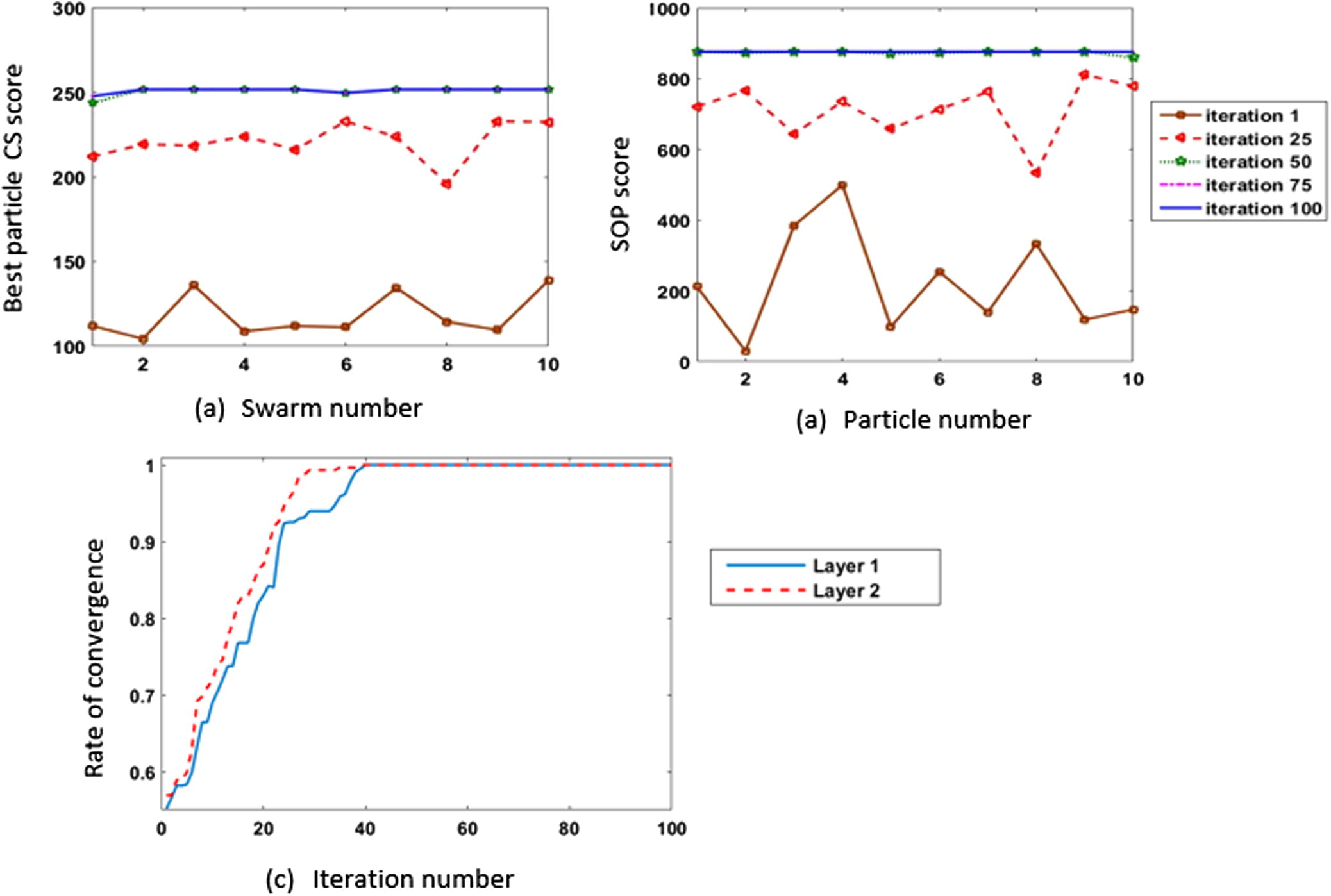

Close

Figure 12

Results of running 100 iterations using 10 particles on 1ezm fragment of length 44.

Export to PPT

Close

Figure 13

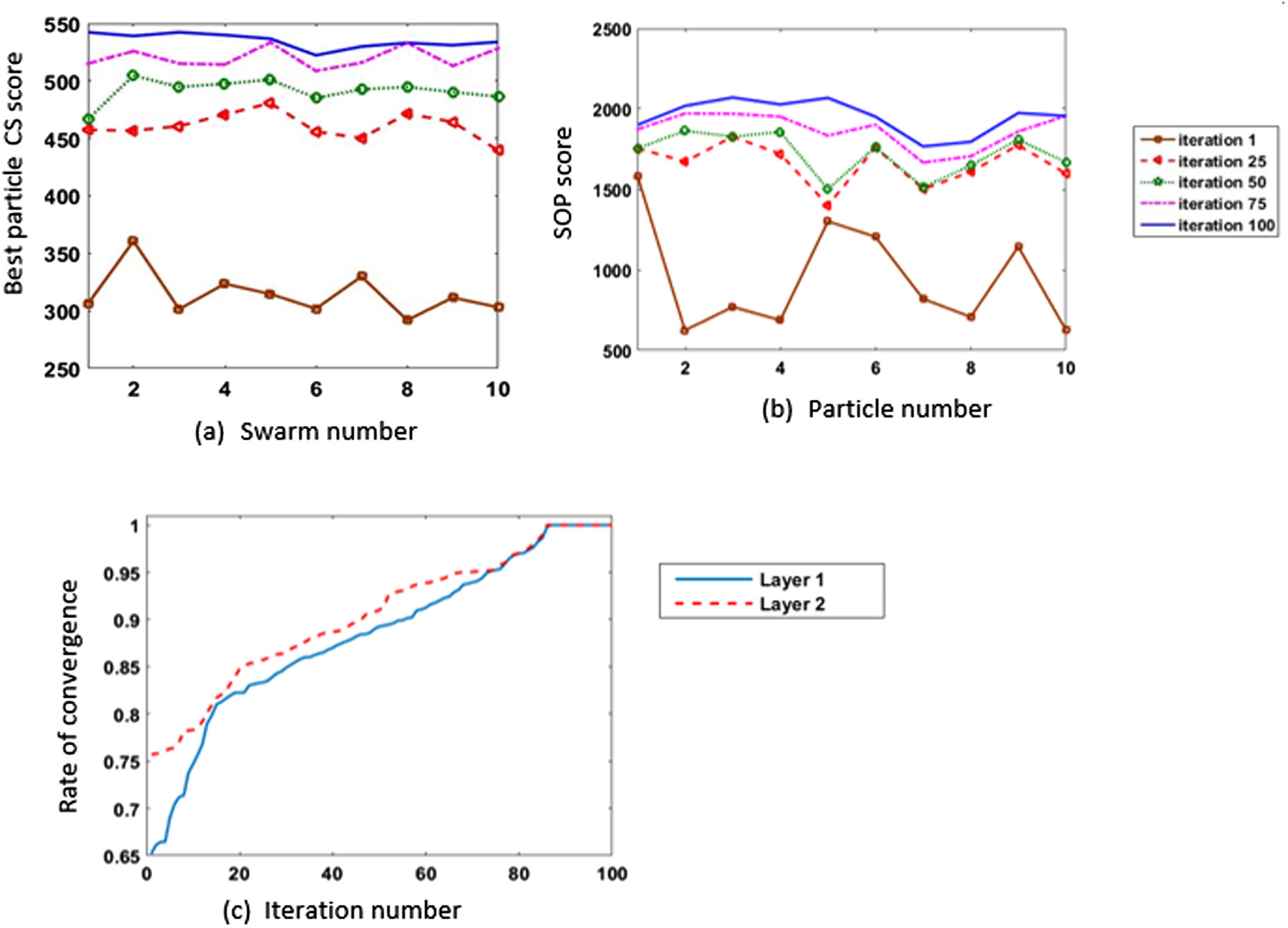
Results of running 100 iterations using 10 particles on 1ppn fragment of length 104.

Export to PPT

6.2

6.2 Parametric study

This section starts with a study for parameters in PSO velocity update equation, with focus on two parameters (velocity clamping, and inertia weight), in Section 6.2.1. In Section 6.2.2, the effectiveness of changing parameters in objective functions is also studied.

6.2.1

6.2.1 PSO parametric study: exploration, and exploitation

PSO, as an optimization technique, is based mainly on two concepts: Exploration, and Exploitation. Exploration is to search within the search space for new optimal solution in the places which have not been visited before. Exploitation is to search for better solution in the places that have been already visited before. Exploration and exploitation are opposite, as increasing exploration will limit the exploitation. Unbalancing between these two concepts may lead the particles to trap in local optima (Chen, and Montgomery, 2013). To achieve good balancing, and avoid premature convergence towards a local optimum, some choices should be decided well, including (Ahmed and Glasgow, 2012):

1. Selection for the suitable values of acceleration coefficient ( $c1$ , $c2$ ).

2. Limiting the particles velocity (velocity clamping).

3. Good selection for inertia weight value.

6.2.1.1

6.2.1.1 Acceleration coefficients

Acceleration coefficients $c1\text{,}c2$ define the ratio of dependency for every particle $m$ in its decision for next position ( $x$ ) on its best position reached ( $\mathit{pbest}$ ) and the globally best position $(\mathit{gbest})$ , respectively, where:

• -

  If $c1$  > c2: it means that particle $m$ will be more biased to its historical best position pbest, to keep diversity of the swarm.

• -

  If $c1$  < c2: it means that particle $m$ will be more biased to the global best position gbest, which helps fast convergence of the swarm (Zhan et al., 2009).

Some experiments by Kennedy (1998) on some typical applications suggest the values of acceleration coefficients $c1$ and $c2$ to be in the range [0, 4], for achieving more control on the search process, where: c1 +  $\mathit{c}\mathit{2}⩽\mathbf{4}$ . Further experiments found the best values for c1, c2 to be: $c1=c2$  = 1.49618 (Eberhart and Shi, 2000).

6.2.1.2

6.2.1.2 Velocity

Velocity $v$ depends on the difference between the current position of the particle and its previous best position $\mathit{pbest}$ , seen in the second (called cognitive) term of Eq. (13), and the difference between the current position of the particle x and its best position reached by the swarm $\mathit{gbest}$ , seen in the third (social) term of the same equation. So, initially, the large difference at the beginning of the iterations leads to larger velocity and more trends towards exploration. As iterations increase, the velocity $\theta$ will be decreased with more trends towards exploitation (Chen and Montgomery, 2013).

In the initial iterations, if the current position $x$ is very large than both $\mathit{pbest}$ and gbest ( $x$  ≫ pbest & $x$  ≫ gbest), that makes the velocity to be largely −ve. In contrast, If the current position $x$ is smaller than both pbest and $\mathit{gbest}$ ( $x$  ≪ pbest & $x$  ≪ gbest), that makes the velocity to be largely +ve. These two large values in velocity may lead to what is called “particle explosion”. That is due to control loss of the velocity magnitude (|v|) which makes the particles leave the search space due to huge steps. To control this problem, velocity clamping is a better solution, which is mentioned in Eqs. (14) and (15).

The parameter $\theta$ in Eq. (14) takes values between [0, 1]. If $\theta$ is large (near to 1), the velocity will be less-controlled, which will lead to particle explosion. Decreasing the value of $\theta$ will lead to more control for the particles. However, if the $\theta$ is set to be very small, that will lead the particle to move very slowly. The slow movement of particles (gaps) allows to explore the search space efficiently, but it takes a long time.

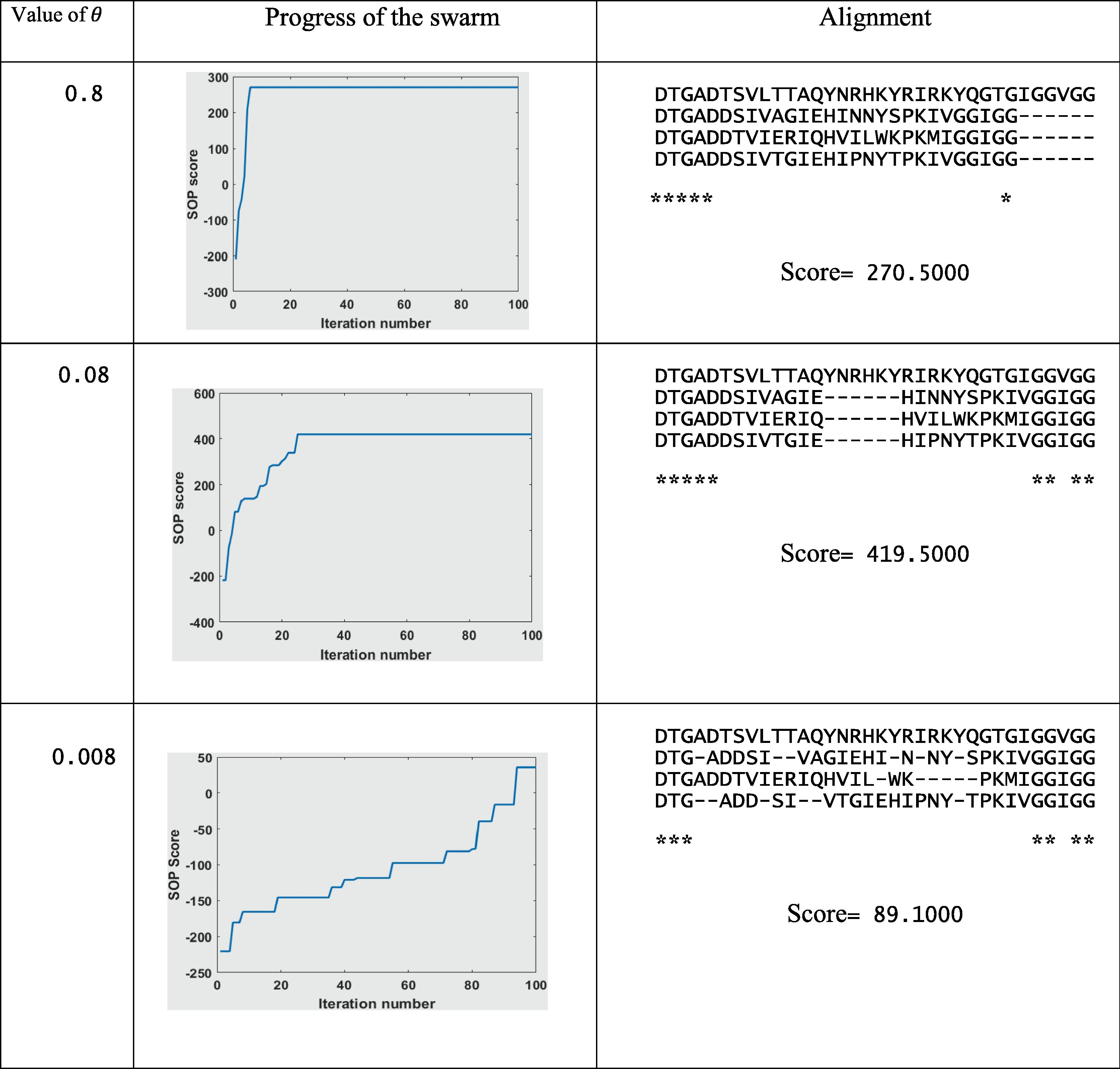
Five values of $\theta$ are run on six Balibase benchmarks. These values are 0.008, 0.03, 0.08, 0.3, and 0.8. Results in Table 2 and Fig. 14 show that the velocity clamping with ( $\theta$  = 0.08) gave the best score. As increase in the $\theta$ value than 0.08, or decreasing it, the scores get worse. That is because while increasing the value of $\theta$ , the system moves towards throwing the gaps at the boundaries of the sequences, and then the system will be trapped. While decreasing the θ value, the gaps move very slowly, and the swarm takes much more time to converge. More illustrated example is seen in Table 3. Table 3 gives results for the alignment of dataset DS1 (which is given in Fig. 15) using three values of $\theta$ (0.8, 0.08, and 0.008). At $\theta$  = 0.8, gaps are being quickly thrown to the boundaries of the search space. By iteration 5, the system has been trapped. At $\theta$  = 0.08, the system reached the optimal solution after a few number of iterations (around 25 iterations). With a very small number of $\theta$  = 0.008, positions of particles are updated very slowly, as by iteration 100, the best particle score was only 89.1. Truly, this system can reach the optimal solution. However, it will need more number of iterations.

Table 2 SOP scores for velocity clamping with different $\theta$ values. Bold font refer to maximum score for each dataset.

Dataset	$\theta$  = 0.8	$\theta$  = 0.3	$\theta$  = 0.08	$\theta$  = 0.03	$\theta$  = 0.008
1fmb	1460	1495	1495	1495	1323.4
1ppn	5035.5	5224.9	5256.1	4886.3	4298.9
1tis	6450.4	7058.7	7224.5	6676	4994.7
1ezm	8077.1	8173.0	8211.8	7283.3	6814.9
1ad3	5373	5409.4	5632.7	5429.6	4975.3
3pmg	7261.6	7856.7	8079.8	7909.2	7081.4

Close

Figure 14

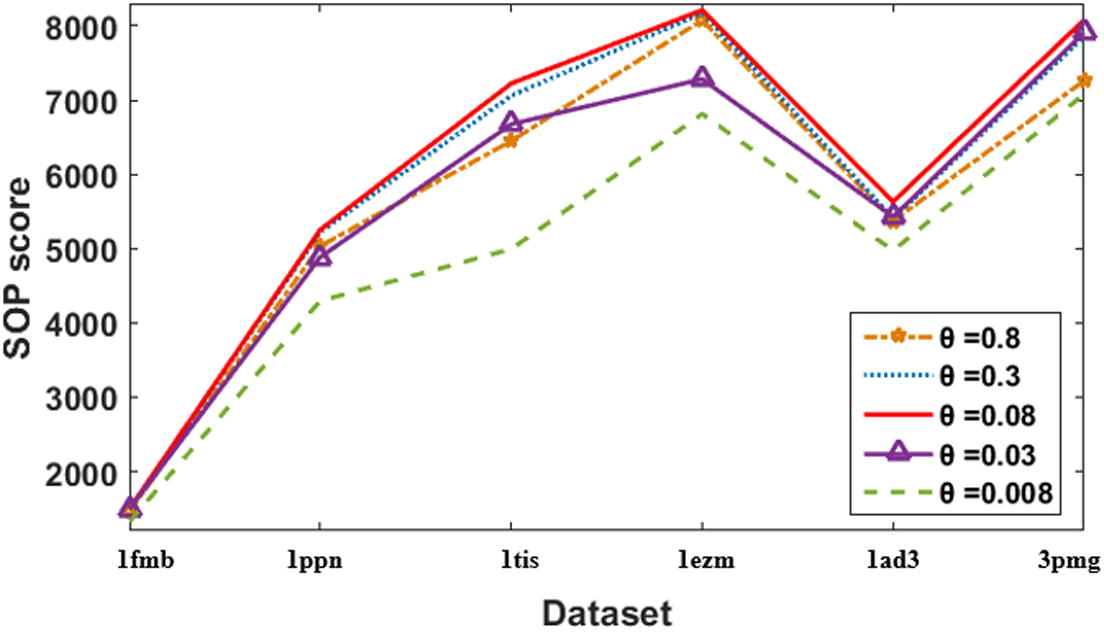
Alignment scores of velocity clamping using different $\theta$ values.

Export to PPT

Table 3 Effectiveness of velocity clamping using different values of $\theta$ on the alignment process.

Close

Figure 15

Two small datasets: DS1, DS2, that will be used in parameters study.

Export to PPT

6.2.1.3

6.2.1.3 Inertia weight

Inertia weight, w, introduced to accelerate the convergence speed of the PSO. It is another way to control the velocity. Probabilities of $w$ can be classified to:

• –

  If $w⩾1$ : the velocity step will be big, and it is hard for the particle to update its direction.

• –

  If $0<w<1$ : it means only a small percentage of the previous velocity $v^{t-1}$ is kept for calculation of the new velocity $v^t$ , with quick ability for particle to change its direction.

• –

  If $w=0$ : the first term in Eq. (13) will be deleted, and so, the second and third terms will be equal to zero when calculating the new velocity of the $\mathit{gbest}$ particle, and so, the particle will not be updated, as $\mathit{gbest}=\mathit{pbest}=x$ .

Changing inertia weight has been tested on many optimization problems and proves its superiority (Kumar et al., 2008). The value of $w$ can be changed by either increasing or decreasing its value every iteration. However, dynamically changing the velocity by decreasing it is better in order to control the balancing between exploration and exploitation (as to start with big to increase exploration, and decrease it till be very small at the end of searching process to increase exploitation). Three weight schemes are tested in this study, which are: decreasing linearly, decreasing nonlinearly, and decreasing exponentially. Exponentially decreased w is previously mentioned in Eq. (16). Decreasing $w$ linearly follows the next equations:

(17)

$$\mathit{step}=\frac{w_o-w_f}{t_{\mathit{max}}}$$

(18)

$$w=w_o-(\mathit{step}\ast t)$$

And nonlinearly decreased value of w follows Eq. (19) as follows:

(19)

$$w=w_f+\left(\frac{w_o-w_f}{t}\right)$$

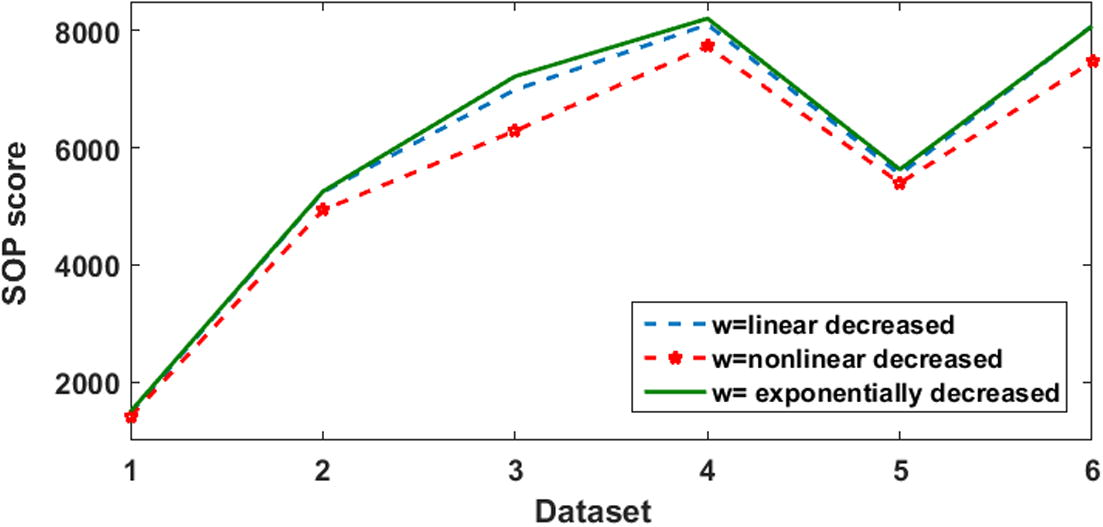
In this experiment, $w$ is decreased from $w_o$  = 0.9, to $w_f$  = 0.4 for all three weighting schemes.

Table 4 and Fig. 16 show that exponentially decreased $w$ was able to reach higher scores than the others two schemes. Only linearly decreased scheme won the exponentially decreased scheme in one dataset with a very little difference.

Table 4 SOP scores for different weight schemes. Bold font refer to maximum score for each dataset.

Dataset	Linearly decreased (0.9:0.4)	Nonlinearly decreased (0.9:0.4)	Exponentially decreased (0.9:0.4)
1fmb	1467.8	1407.7	1495
1ppn	5245.9	4937.3	5256.1
1tis	6994.7	6292.5	7224.5
1ezm	8106.8	7737.3	8211.8
1ad3	5549	5399.7	5632.7
3pmg	8089.9	7471.7	8079.8

Close

Figure 16

Alignment scores of different weight schemes.

Export to PPT

6.2.2

6.2.2 Objective functions parametric study

In this paper, two scoring functions are used. The first is (CS) score (Eq. (1)), which doesn’t contain parameter to be tuned. So, this section will focus on the second objective function (SOP), especially on the selection of gap penalty scores.

There are different conventions regarding the gap penalty such as linear gap penalty, and affine gap penalty. In linear gap penalty, each gap is given a penalty such that all gaps are equal in punishment value either this gap is an open of the gap series ℓ, or not. This makes no control on the place of the gaps. However, biologically, the possibility of having a single long gap $\ell$ in the protein sequence is more likely to occur than the multiple small series of gaps (Gotoh, 1983). That is because if a deletion for an amino acid is created once, it is easy to be extended. For that reason, this paper used the affine gap penalty (Eq. (4)) generated by Gotoh (1983).

Increasing the value of gap open penalty go will lead to a reduction in the numbers of opening gaps, and the system will move towards increasing the length of a gap ℓ. Dataset DS1 (shown in Fig. 15) is aligned three times using different gap open penalty values (−2, −6, and −10), as in Fig. 17. Although a low value of a gap open penalty may lead to more matches, it is in contrary to the biological information. Biologically, the probability that the amino acid R (in bold) was H, and has been mutated is more likely to happen. Also, it is the case with (V) in bold as it once was (I) and has been mutated. That is why this paper used a gap open penalty $\mathit{go}$ of −10.

Close

Figure 17

Optimal alignment on DS1 using different gap open penalty scores.

Export to PPT

According to gap extension penalty ge, its value affects the number of gaps in the alignment. Dataset DS2 (in Fig. 15) is aligned using a fixed $\mathit{go}$ , with different values. As shown in Fig. 18, when for example $\mathit{ge}$ is set to be −3, the relatively high value of $\mathit{ge}$ forced the system to use more numbers of gaps, and forbade the system from achieving more matches. However, with a low value of −1, more gaps were added, with more matches.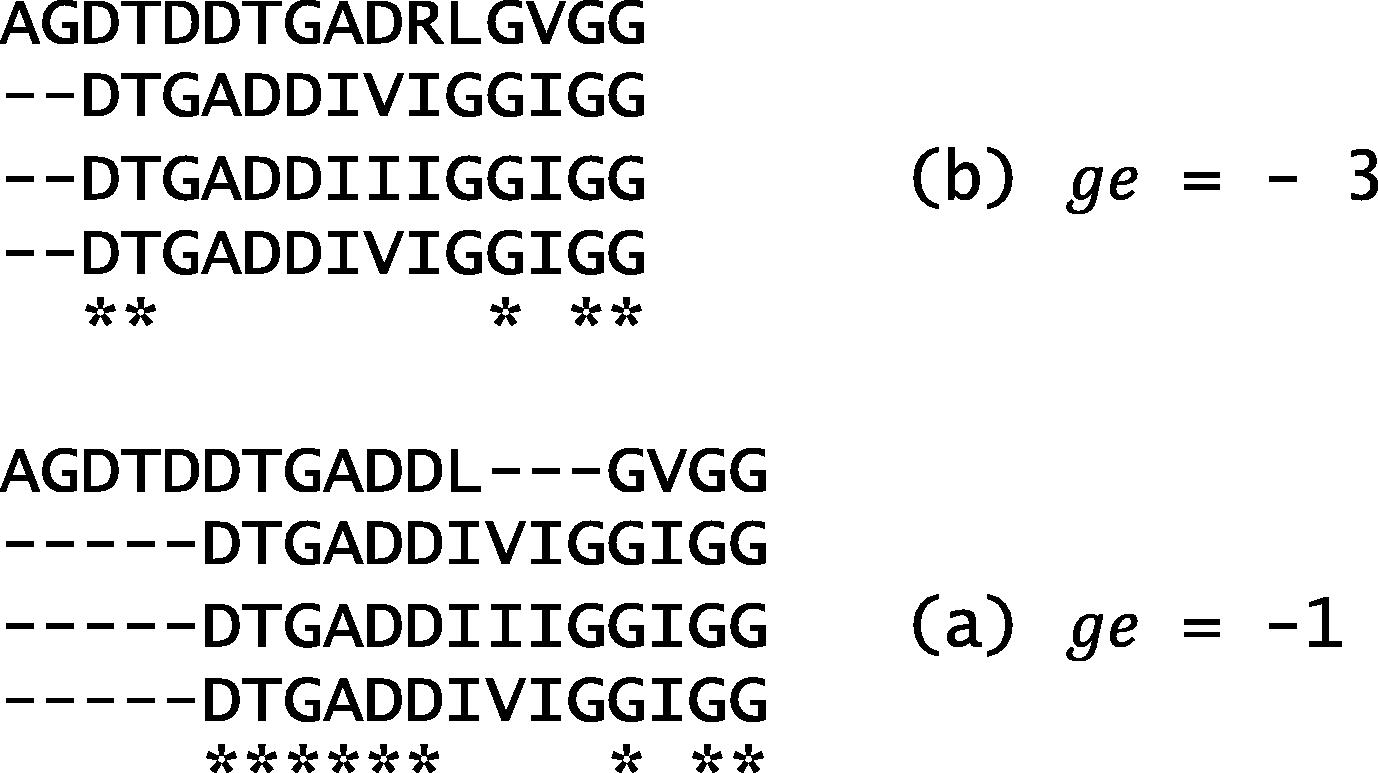

Close

Figure 18

Optimal alignment on DS2 using different gap extension penalty scores.

Export to PPT

7 Conclusion

This paper proposed FTLPSO algorithm as a contribution for solving the MSA problem. The algorithm has two main steps: the first is fragmentation of long sequences, and the second is aligning each fragment alone using two-layer PSO (TLPSO) structure. Fragmentation helps the PSO to deal with short sequences. TLPSO is a good selection for solving MSA as unconstrained problems. Solving MSA problem requires maximization of column score (CS), as maximizing sum of pair score (SOP). The first layer in TLPSO structure contains a number of swarms, which deals with the CS scoring function. The swarm in the second layer is dealing with SOP scoring function. In every swarm, local PSO and best particle mutation are applied to keep particles far from trapping in a local optima as possible. FTLPSO is run on 6 datasets from balibase reference, and the results are compared with five state-of-the-art tools: CLUSTAL Omega, CLUSTAL W2, TCOFFEE, KALIGN, and DIALIGN-PFAM. FTLPSO overcame other tools and could keep the score high in all tested datasets. It also achieved the best average score among them. After comparing the proposed method with other tools, a parametric study is applied which proofs the efficiency of the used values in the updating equation for PSO as in the objective function used.

As a future path of this work is to focus on studying the efficiency of different fragmentation techniques instead of $k$ -tuple, decreasing the memory usage, CPU usage, and increasing the processing time are the main interest as future works.