A comparison of HPM, NDHPM, Picard and Picard–Padé methods for solving Michaelis–Menten equation

H. Vazquez-Leal; J. Rashidinia; L. Hernandez-Martinez; H. Daei-Kasmaei

doi:10.1016/j.jksus.2014.11.001

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original article

27 (

); 7-14

doi:

10.1016/j.jksus.2014.11.001

A comparison of HPM, NDHPM, Picard and Picard–Padé methods for solving Michaelis–Menten equation

H. Vazquez-Leal^{^a,*}, J. Rashidinia^{^b}, L. Hernandez-Martinez^{^c}, H. Daei-Kasmaei^{^b}

a Electronic Instrumentation and Atmospheric Sciences School, University of Veracruz, Cto. Gonzalo Aguirre Beltrán S/N, Xalapa 91000, Veracruz, Mexico

b Department of Mathematics and Statistics, Faculty of Basic Science, Islamic Azad University, Central Tehran Branch, P.O. Box 13185.768, Tehran, Iran

c National Institute for Astrophysics, Optics and Electronics, Luis Enrique Erro #1, Sta. María Tonantzintla 72840, Puebla, Mexico

*Corresponding author hvazquez@uv.mx (H. Vazquez-Leal)

Received: 2014-7-9, Accepted: 2014-11-2, Published: 2014-01-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Available online 14 November 2014

Peer review under responsibility of King Saud University.

Abstract

The fact that physical phenomena are modelled, mostly, by nonlinear differential equations underlines the importance of having reliable methods to solve them. In this work, we present a comparison of homotopy perturbation method (HPM), nonlinearities distribution homotopy perturbation method (NDHPM), Picard, and Picard–Padé methods to solve Michaelis–Menten equation. The results show that NDHPM possesses the smallest average absolute relative error 1.51(−2) of all tested methods, in the range of $r \in [0, 5]$ . Also, we introduce the combination of Picard’s iterative method and Padé approximants as an alternative to reduce complexity of Picard’s solutions and increase accuracy.

Keywords

Homotopy perturbation method

Picard’s method

Padé

Michaelis–Menten

Show Related Articles from PubMed

1 Introduction

Many important physical phenomena on the engineering and science fields are frequently modelled by nonlinear differential equations. Such equations are often difficult or impossible to solve analytically. Nevertheless, analytical approximate methods to obtain approximate solutions have gained importance in recent years. There are several methods employed to find approximate solutions to nonlinear problems like homotopy perturbation method (HPM) He (2004, 2009, 1999), Biazar and Aminikhah (2009), Biazar and Ghazvini (2009a), Koak et al. (2011), Vázquez-Leal et al. (2012), Vazquez-Leal et al. (2012a), Filobello-Nino et al. (2012b), Khan et al. (2011a), Biazar and Ghazvini (2008, 2009b), Sheikholeslami et al. (2012), Filobello-Nino et al. (2012a), Picard’s iterative method Ramos (2009), Szinvelski et al. (2006), Layton and Lenferink (1995), Rach (1987), Bellomo and Sarafyan (1987), Lal and Moffatt (1982), Adomian decomposition method El-Sayed et al. (2010), Li (2009), Ezzati and Shakibi (2011), Safari et al. (2009), Hojjati and Jafari (2008), Abidi and Omrani (2010), homotopy analysis method (HAM) Rashidi and Dinarvand (2009), Bataineh et al. (2009), Abbasbandy and Shivanian (2011), Tan and Abbasbandy (2008), Mastroberardino (2011), Abbasbandy (2008), Shukla et al. (2012), Gorder and Vajravelu (2009), Chen and Liu (2008), Qian and Chen (2010), Abbasbandy (2010), Wang (2011), Varitional iteration method He (2012), Turkyilmazoglu (2011), Geng (2011), Altintan and Ugur (2009), Shang and Han (2010), Chen and Wang (2010), Saadati et al. (2009), Odibat and Momani (2009), among others. In this paper, we will present a comparison of nonlinearities distribution homotopy perturbation method (NDHPM) Vazquez-Leal et al. (2012a), Filobello-Nino et al. (2014), homotopy perturbation method, Picard’s method and Picard–Padé method to solve Michaelis–Menten equation Golinik (2010, 2011), Gonzalez-Parra et al. (2011). The obtained results show that NDHPM possesses the smallest average absolute relative error 1.51(−2) in the range of $r \in [0, 5]$ . In addition, we introduce the combination of Picard’s iterative method and Padé approximants as an alternative to reduce complexity of Picard’s solutions in order to increase accuracy.

This paper is organized as follows. In Section Appendix A, we introduce the basic idea of HPM method. Section 2 presents the basic concept of NDHPM method. We introduce the Picard–Padé coupled method in Section 3. Section 4 presents the approximated solutions of a case study by NDHPM, HPM, Picard and Picard–Padé methods. In Section 5, numerical illustrations are performed and the results discussed. Finally, a brief conclusion is given in Section 6.

2 Distribution of nonlinearities for HPM method (NDHPM)

A recent report Vazquez-Leal et al. (2012a), Filobello-Nino et al. (2014) introduced the NDHPM method, which eases the searching process of solutions for (A.3) and reduces the complexity when solving differential equations. As first step, the homotopy of the form Vazquez-Leal et al. (2012a) is introduced

(1)

H (v, p) = (1 - p) [L (v) - L (u_{0})] + p (L (v) + N (v, p) - f (r, p)) = 0, p \in [0, 1] .

It can be noticed that the homotopy function (1) is essentially the same as (A.4), except for the non-linear operator N and the non-homogeneous function f, which contain the embedded homotopy parameter p. The arbitrary introduction of p within the differential equation is a strategy to redistribute the nonlinearities between the successive iterations of the HPM method, and thus, increase the probabilities of finding the sought solution.

Again, we establish that

(2)

v = \sum_{i = 0}^{\infty} v_{i} p^{i},

when

p \to 1

, it turns out that the approximate solution for (A.1) is

(3)

u = \lim_{p \to 1} v = \sum_{i = 0}^{\infty} v_{i} .

3 Picard method and Padé aftertreatment

Given a first order nonlinear differential equation, it can be expressed as

(4)

y^{'} (r) = L + N + f (r),

having initial conditions

(5)

y (r^{*}) = K,

where L is a linear operator, N is a nonlinear operator, and

f (r)

is a known function for the independent variable r.

The basic formulation of Picard iterative method is

(6)

y_{i + 1} (r) = K + \int_{r^{*}}^{r} y_{i} (v) dv,

where the last equation involves n integrals,

y_{i}

is the right side of Eq. (4), and

r^{*}

is the expansion point.

Usually, the application of Picard’s method generates large mathematical expressions difficult to handle. Therefore, we propose the use of a coupling between Picard’s method and Padé approximants to generate compact expressions on one hand and increase accuracy Khader (2012) on the other.

3.1

3.1 Padé approximants

A rational approximation to $f (r)$ on $[a, b]$ is the quotient of two polynomials $P_{N} (r)$ and $Q_{M} (r)$ of degrees N and M, respectively. We use the notation $R_{N, M} (r)$ to denote this quotient. The $R_{N, M} (r)$ Padé Merdan et al. (2011), Baker (1975), Khader (2012), Noor and Mohyud-Din (2009), Bararnia et al. (2012), Raftari and Yildirim (2011), Sangaranarayanan and Rajendran (1997), Nallasamy and Rajendran (1998), Rajendran (2000) approximation to a function $f (r)$ has been given by

(7)

R_{N, M} = \frac{P_{N} (r)}{Q_{M} (r)} for a ⩽ r ⩽ b .

The method of Padé requires that $f (r)$ and its derivatives be continuous at $r = 0$ . The polynomials used in (7) are defined as follows

(8)

P_{N} (r) = p_{0} + p_{1} r + p_{2} r^{2} + \dots + p_{N} (r^{N}),

(9)

Q_{M} (r) = q_{0} + q_{1} r + q_{2} r^{2} + \dots + q_{M} (r^{M}) .

The polynomials in (8) and (9) are constructed so that $f (r), R_{N, M} (r)$ , and their derivatives up to $N + M$ are equal at $r = 0$ . For the case when $q_{0} = 1$ , the approximation is only the Maclaurin expansion for $f (r)$ . For a fixed value of $N + M$ , the error is the lowest when $P_{N} (r)$ and $Q_{M} (r)$ have the same degree or when $P_{N} (r)$ is one degree higher than $Q_{M} (r)$ .

Notice that the constant coefficients of $Q_{M}$ are M. This is permissible because 0 and $R_{N, M} (r)$ are not changed when both $P_{N} (r)$ and $Q_{M} (r)$ are divided by the same constant. Hence, the rational function $R_{N, M} (r)$ has $N + M + 1$ unknown coefficients. Assuming that $f (r)$ is analytic and has the Maclaurin expansion

(10)

f (x) = a_{0} + a_{1} r + a_{2} r^{2} + \dots + a_{k} r^{k} + \dots,

and from the difference

f (r) Q_{M} (r) - P_{N} (r) = Z (r)

(11)

⌈\sum_{i = 0}^{\infty} a_{i} r^{i}⌉ ⌈\sum_{i = 0}^{M} q_{i} r^{i}⌉ - ⌈\sum_{i = 0}^{N} p_{i} r^{i}⌉ = ⌈\sum_{i = N + M + 1}^{\infty} c_{i} r^{i}⌉ .

The lower index $i = N + M + 1$ in the summation at the right side of (11) is chosen because the first $N + M$ derivatives of $f (r)$ and $R_{N, M} (r)$ should agree at $r = 0$ .

When the left side of (11) is multiplied out and coefficients of the $r^{i}$ powers are set equal to zero for $i = 0, 1, \dots, N + M$ , a system of $N + M + 1$ linear equations produced is as follows:

(12)

\begin{matrix} a_{0} - p_{0} = 0, \\ q_{1} a_{0} + a_{1} - p_{1} = 0, \\ q_{2} a_{0} + q_{1} a_{1} + a_{2} - p_{2} = 0, \\ q_{3} a_{0} + q_{2} a_{1} + q_{1} a_{2} + a_{3} - p_{3} = 0, \\ q_{M} a_{N - M} + q_{M - 1} a_{N - M - 1} + a_{N} - p_{N} = 0, \end{matrix}

and

(13)

\begin{matrix} q_{M} a_{N - M + 1} + q_{M - 1} a_{N - M + 2} + \dots + q_{1} a_{N} + a_{N + 2} = 0, \\ q_{M} a_{N - M + 2} + q_{M - 1} a_{N - M + 3} + \dots + q_{1} a_{N + 1} + a_{N + 3} = 0, \\ ⋮ \\ q_{M} a_{N} + q_{M} a_{N + 1} + \dots + q_{1} a_{N + M + 1} + a_{N + M} = 0 . \end{matrix}

Notice that in each equation, the sum of indices on the factors for each product is the same and this sum increases, consecutively, from 0 to $N + M$ . The M equations in (13) involve only the unknowns $q_{1}, q_{2}, \dots, q_{M}$ and must be solved first. Then, equations in (12) are used successively to find $p_{1}, p_{2}, \dots, p_{N}$ Merdan et al. (2011).

4 Solution of Michaelis–Menten equation

The Michaelis–Menten (MM) equation is employed to describe the kinetics of enzyme-catalysed reactions. Enzymes are proteins that catalyse the chemical reactions essential for living organisms. Therefore, we will solve the MM equation Golinik (2010, 2011), Gonzalez-Parra et al. (2011) nonlinear differential equation by using NDHPM, HPM, and Picard–Padé methods. The formulation of Michaelis–Menten problem is

(14)

s^{'} (r) = - \frac{V_{m} s (r)}{K_{m} + s (r)}, s (0) = a,

where

s (r)

is the substrate concentration;

V_{m}

and

K_{m}

are the limiting rate and Michaelis constant, respectively. In general, the explicit closed form of Eq. (14) is given as follows:

(15)

s (r) = K_{m} W \{\frac{a}{K_{m}} \exp (\frac{a - V_{m} r}{K_{m}})\}

where W is the Lambert function and a is a constant value from initial condition that satisfies in Eq. (14)Vazquez-Leal et al. (2012b).

Now in Eq. (14) , we choose $a = 1, K_{m} = 2$ and $V_{m} = 1$ . In this case, the explicit closed-form solution for (14) is

(16)

s (r) = \exp (- W (\frac{1}{2} \exp (\frac{1}{2} r + \frac{1}{2})) + \frac{1}{2} r + \frac{1}{2}),

In order to apply all the methods under test, we propose the use of a seventh order Taylor series expansion of rational term from MM equation. Then, (14) is reformulated as

(17)

\begin{matrix} s^{'} (r) - \frac{1}{2} s (r) + \frac{1}{4} s {(r)}^{2} - \frac{1}{8} s {(r)}^{3} + \frac{1}{16} s {(r)}^{4} - \frac{1}{32} s {(r)}^{5} + \frac{1}{64} s {(r)}^{6} = 0, \\ s (0) = 1, \end{matrix}

4.1

4.1 Solution by NDHPM method

By using (1) and (17), we establish the following homotopy equation

(18)

H (r, p) = (1 - p) (L (v) - L (u_{0})) + p (v^{'} - \frac{1}{2} v + \frac{1}{4} v^{2} p - \frac{1}{8} v^{3} p^{2} + \frac{1}{16} v^{4} p^{3} - \frac{1}{32} v^{5} p^{4} + \frac{1}{64} v^{6} p^{5}) = 0,

where the linear operator L and trial function

u_{0}

are chosen as (A.10) and (A.11), respectively.

Substituting (2) into (18), reordering, and equating terms having the same p-powers, we obtain the following system of linear differential equations

(19)

\begin{matrix} 2 v_{1}^{'} - 2 {Cv}_{1} - v_{0}^{'} + 2 {Cv}_{0} - \frac{1}{2} v_{0} = 0, v_{1} (0) = 0, \\ 2 v_{2}^{'} - \frac{1}{2} v_{1} - 2 {Cv}_{2} + 2 {Cv}_{1} + \frac{1}{4} v_{0}^{2} - v_{1}^{'} = 0, v_{2} (0) = 0, \\ 2 v_{3}^{'} - \frac{1}{8} v_{0}^{3} - \frac{1}{2} v_{2} + \frac{1}{2} v_{0} v_{1} - v_{2}^{'} + 2 {Cv}_{2} - 2 {Cv}_{3} = 0, v_{3} (0) = 0 . \end{matrix}

Solving (19), yields

(20)

\begin{matrix} v_{1} = - \frac{2 C - 1}{4} r \exp (Cr), \\ v_{2} = \frac{\exp (Cr)}{32 C} (- 4 C^{2} r^{2} + {Cr}^{2} + 4 C^{3} r^{2} - 4 \exp (Cr) - 8 C^{2} r + 4 Cr + 4), \end{matrix}

(21)

v_{3} = - \frac{\exp (Cr)}{384 C^{2}} (- 12 C^{2} r^{2} + 48 C^{3} r^{2} - 48 \exp (Ct) C^{2} r + 48 C \exp (Cr) - 48 C^{4} r^{2} + 8 C^{5} r^{3} - 12 \exp (2 Cr) C + 6 C^{3} r^{3} + 48 C^{3} r - 12 {CrC}^{2} r^{3} - 12 C^{4} r^{3} - 12 \exp (Cr) + 24 \exp (Cr) Cr - 36 C + 12) .

We are able establish the first, second, and third order approximations of $s (r)$ as

(22)

\lim_{p \to 1} (\sum_{i = 0}^{1} v_{i} p^{i}) = v_{0} + v_{1},

(23)

\lim_{p \to 1} (\sum_{i = 0}^{2} v_{i} p^{i}) = v_{0} + v_{1} + v_{2},

and

(24)

\lim_{p \to 1} (\sum_{i = 0}^{3} v_{i} p^{i}) = v_{0} + v_{1} + v_{2} + v_{3},

respectively.

4.2

4.2 Solution by Picard–Padé method

For this case we use (6) and (17), establishing the following iterative integral equation

(25)

s_{i + 1} = 1 + \int_{0}^{t} (\frac{1}{2} s_{i} - \frac{1}{4} s_{i}^{2} + \frac{1}{8} s_{i}^{3} - \frac{1}{16} s_{i}^{4} + \frac{1}{32} s_{i}^{5} - \frac{1}{64} s_{i}^{6}) dv,

where as trial function we choose

s_{0} = u_{0} (v)

(see Eq. (A.11)).

Now, after performing three iterations, we obtain

(26)

\begin{matrix} s_{1} (r) = 1 - r (\frac{1}{4} \exp (2 Cr) - \frac{1}{64} \exp (6 Cr) + \frac{1}{8} \exp (3 Cr) \\ + \frac{1}{32} \exp (5 Cr) + \frac{1}{2} \exp (Cr) - \frac{1}{16} \exp (4 Cr)) \\ ⋮ \end{matrix}

We calculated the three iterations using Maple software. However, due to space constraints, we do not show terms

s_{2} (r)

and

s_{3} (r)

because the size of resultant expressions is too large. Next, we apply Padé approximant of order [8,8] to

s_{3} (r)

, the result is

(27)

{\hat{s}}_{3} (r) = \frac{1 - \frac{28}{23} r + \frac{148}{247} r^{2} - \frac{15}{127} r^{3} + \frac{7}{575} r^{4} - \frac{1}{546} r^{5} + \frac{1}{2704} r^{6} + \frac{1}{3018} r^{7} + \frac{1}{3119} r^{8}}{1 - \frac{17}{11} r + \frac{23}{22} r^{2} - \frac{14}{39} r^{3} + \frac{9}{133} r^{4} - \frac{1}{120} r^{5} + \frac{1}{751} r^{6} + \frac{1}{2548} r^{7} + \frac{1}{13890} r^{8}} .

5 Numerical illustration and discussion

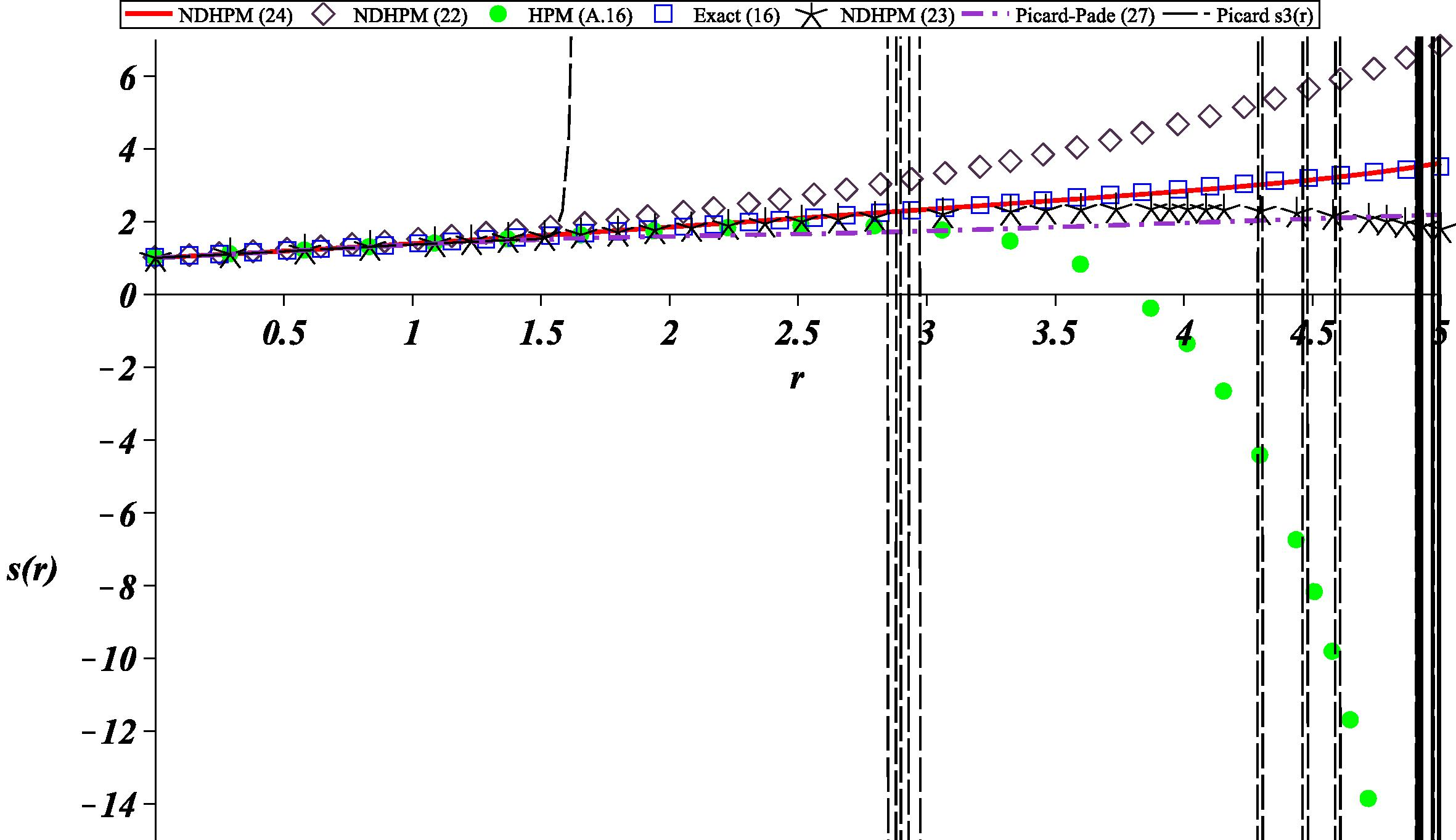
Fig. 1 and Table 1 show a comparison between the exact solution (16) for the nonlinear differential Eq. (14) and the analytic approximation methods (A.16), (22), (23), (24), Picard $s_{3} (r)$ , and (27).

Exact solution (16) (box) for (14) and approximate solutions (A.16) (solid circles), (20) (diamonds), (23) (asterisk), (solid line) (24) Picard s 3 ( r ) (long-dash) and Picard Padé (dash-dot) (27).

Table 1 Comparison between exact solution (16) and the approximation results obtained by HPM (A.16), NDHPM (22)–(24), third order Picard

s_{3} (r)

and Picard–Padé (27).

r	Exact (16)	NDHPM (24)	NDHPM (23)	NDHPM (22)
0.5	1.1759119876	1.1855837778	1.1724798244	1.2210299969
1.0	1.3701538843	1.3908420392	1.3629264319	1.4876439201
1.5	1.5822739533	1.6129786189	1.5678227124	1.8088455412
2.0	1.8115900830	1.8475639712	1.7802218782	2.1953653632
2.5	2.0572549291	2.0890094641	1.9880649474	2.6599847443
3.0	2.3183170092	2.3322211070	2.1718046811	3.2179198792
3.5	2.5937729182	2.5765507361	2.3010703654	3.8872765515
4.0	2.8826086613	2.8339975240	2.3300097350	4.6895885402
4.5	3.1838301540	3.1450071692	2.1908106843	5.6504548846
5.0	3.4964841372	3.6075242101	1.7847234646	6.8002939495

	Order	3	2	1
	A.A.R.E	0.0151	0.124	0.401

r	HPM(A.16)	Picard–Padé(27)	Picard $s_{3} (r)$
0.5	1.1676449955	1.1770908197	1.177572198
1.0	1.3536430476	1.3605873679	1.364655683
1.5	1.5518481099	1.5074531253	1.530802672
2.0	1.7426139870	1.5945279183	−1.331232(+10)
2.5	1.8705654981	1.6524134970	−6.439854(+21)
3.0	1.7860856968	1.7358003068	−7.010528(+34)
3.5	1.0919411260	1.8428178198	6.122727(+48)
4.0	−1.2568485461	1.9590309606	−5.899544(+61)
4.5	−7.9918998337	2.0752755420	−2.074249(+75)
5.0	−26.216385114	2.1870250462	−5.750278(+90)

Order	1	3	3
A.A.R.E	1.44	0.196	1.644(+89)

From Fig. 1, we can observe that NDHPM solution of orders: 1, 2, and 3 gradually overlaps with exact solution. In fact, NDHPM solution possesses the lowest average absolute relative error (A.A.R.E) from all approximations 0.0151 (see Table 1). The nonlinearities distribution of NDHPM method helps to simplify the solution process of the differential equations. If we compare the differential equations of HPM (A.12), (A.13), (A.14) and NDHPM (19), we can notice that the NDHPM equations are more compact and easy to handle. As a matter of fact, HPM iterations of (A.13) and (A.14) do not possess explicit closed solutions, otherwise, the second and third order equations from NDHPM have solutions (see (20)).

The approximation of Picard $s_{3} (r)$ has a good fitting until $r = 2$ . After that point, this approximation diverges from exact solution, reaching the highest A.A.R.E. $1.644 (+ 89)$ . The expression of $s_{3} (r)$ contains a very large number of exponential and polynomial terms causing the notorious A.A.R.E. Nevertheless, by means of coupling Picard and Padé, we can obtain an accurate approximation (27); besides, it is a compact rational expression, more handy and faster to evaluate than $s_{3} (r)$ .

On one hand, we showed that NDHPM is a good modification to the HPM method; useful to obtain higher order approximate solutions for nonlinear differential equations. In particular, NDHPM can solve non-linear problems that includes transcendental functions, rational expressions or combinations of both. Moreover, NDHPM requires the arbitrary embedding of the homotopy parameter inside the nonlinear operator. Then, further work should be done to propose a systematic methodology for the embedding process for p. On the other hand, we showed that the coupling of Picard method and Padé approximants is helpful to calculate compact expressions with lower absolute error. Future work should be done to improve Picard–Padé method in order to improve the accuracy of solutions.

6 Conclusions

This work presented a comparison of HPM, NDHPM, Picard, and Picard–Padé methods by solving the Michaelis–Menten equation. We showed that NDHPM is the best of the tested methods. In particular, it is useful to solve non-linear problems that include transcendental functions, rational expressions, or combinations of both. NDHPM helps to obtain higher order approximations and better accuracy, even more compact expressions than HPM method. NDHPM requires the arbitrary embedding of the homotopy parameter inside the nonlinear operator, however. Further work should be done to propose a systematic methodology of the embedding process for p. Besides, we showed that coupling Picard’s method and Padé approximants can be helpful to calculate compact expressions with less absolute error. Further work should be done to improve Picard–Padé method in order to increase the accuracy of solutions.

Disclosure policy

The authors declare that they have no conflict of interest.

Acknowledgments

We gratefully acknowledge the financial support provided by the National Council for Science and Technology of Mexico (CONACyT) through grant CB-2010-01 #157024. Authors wish to acknowledge U. Filobello-Nino, R. Castaneda-Sheissa, R.A. Callejas-Molina, and R. Ruiz-Gomez for their contribution to this project.

References

Abbasbandy S., . Approximate solution for the nonlinear model of diffusion and reaction in porous catalysts by means of the homotopy analysis method. Chem. Eng. J.. 2008;136:144-150.
[Google Scholar]
Abbasbandy S., . Homotopy analysis method for the Kawahara equation. Nonlinear Anal. Real World Appl.. 2010;11:307-312.
[Google Scholar]
Abbasbandy S., Shivanian E., . Predictor homotopy analysis method and its application to some nonlinear problems. Commun. Nonlinear Sci. Numer. Simul.. 2011;16:2456-2468.
[Google Scholar]
Abidi F., Omrani K., . The homotopy analysis method for solving the Fornberg Whitham equation and comparison with Adomianan’s decomposition method. Comput. Math. Appl.. 2010;59:2743-2750.
[Google Scholar]
Altintan D., Ugur O., . Variational iteration method for SturmLiouville differential equations. Comput. Math. Appl.. 2009;58:322-328.
[Google Scholar]
Baker G., . Essentials of Padé Approximations. New York: Academic Express; 1975.
Bararnia H., Ghasemi E., Soleimani S., Ghotbi A.R., Ganji D., . Solution of the Falknerskan wedge flow by HPM Padé method. Adv. Eng. Softw.. 2012;43:44-52.
[CrossRef] [Google Scholar]
Bataineh A.S., Noorani M., Hashim I., . On a new reliable modification of homotopy analysis method. Commun. Nonlinear Sci. Numer. Simul.. 2009;14:409-423.
[Google Scholar]
Bellomo N., Sarafyan D., . On Adomian’s decomposition method and some comparisons with Picard’s iterative scheme. J. Math. Anal. Appl.. 1987;123:389-400.
[Google Scholar]
Biazar J., Aminikhah H., . Study of convergence of homotopy perturbation method for systems of partial differential equations. Comput. Math. Appl.. 2009;58:2221-2230.
[Google Scholar]
Biazar J., Ghazvini H., . Numerical solution for special non-linear Fredholm integral equation by HPM. Appl. Math. Comput.. 2008;195:681-687.
[Google Scholar]
Biazar J., Ghazvini H., . Convergence of the homotopy perturbation method for partial differential equations. Nonlinear Anal. Real World Appl.. 2009;10:2633-2640.
[Google Scholar]
Biazar J., Ghazvini H., . He’s homotopy perturbation method for solving systems of Volterra integral equations of the second kind. Chaos Solitons Fractals. 2009;39:770-777.
[Google Scholar]
Chen X., Wang L., . The variational iteration method for solving a neutral functional–differential equation with proportional delays. Comput. Math. Appl.. 2010;59:2696-2702.
[Google Scholar]
Chen Y., Liu J., . Homotopy analysis method for limit cycle flutter of airfoils. Appl. Math. Comput.. 2008;203:854-863.
[Google Scholar]
El-Sayed A., Behiry S., Raslan W., . Adomian’s decomposition method for solving an intermediate fractional advection dispersion equation. Comput. Math. Appl.. 2010;59:1759-1765.
[Google Scholar]
Ezzati R., Shakibi K., . Using Adomian’s decomposition and multiquadric quasi-interpolation methods for solving NewellWhitehead equation. Proc. Comput. Sci.. 2011;3:1043-1048.
[Google Scholar]
Faraz N., Khan Y., . Analytical solution of electrically conducted rotating flow of a second grade fluid over a shrinking surface. Ain Shams Eng. J.. 2011;2:221-226.
[Google Scholar]
Filobello-Nino U., Vazquez-Leal H., Khan Y., Castaneda-Sheissa R., Yildirim A., Hernandez-Martinez L., Sanchez-Orea J., Castaneda-Sheissa R., Bernal F.R., . HPM applied to solve nonlinear circuits: a study case. Appl. Math. Sci.. 2012;6:4331-4344.
[Google Scholar]
Filobello-Nino U., Vazquez-Leal H., Castaneda-Sheissa R., Yildirim A., Hernandez-Martinez L., Pereyra-Diaz D., Perez-Sesma A., Hoyos-Reyes C., . An approximate solution of Blasius equation by using HPM method. Asian J. Math. Statist.. 2012;5:50-59.
[Google Scholar]
Filobello-Nino U., Vazquez-Leal H., Khan Y., Pereyra-Diaz D., Perez-Sesma A., Diaz-Sanchez A., Jimenez-Fernandez V., Herrera-May A., Lopez-Martinez R., Sanchez-Orea J., . Nonlinearities distribution homotopy perturbation method as a tool to find power series solutions to differential equations. Nova Sci.. 2014;12:13-28.
[Google Scholar]
Geng F., . A piecewise variational iteration method for treating a nonlinear oscillator of a mass attached to a stretched elastic wire. Comput. Math. Appl.. 2011;62:1641-1644.
[Google Scholar]
Golinik M., . Explicit reformulations of time-dependent solution for a Michaelis Menten enzyme reaction model. Anal. Biochem.. 2010;406:94-96.
[Google Scholar]
Golinik M., . Evaluation of enzyme kinetic parameters using explicit analytic approximations to the solution of the Michaelis Menten equation. Biochem. Eng. J.. 2011;53:234-238.
[Google Scholar]
Gonzalez-Parra G., Acedo L., Arenas A., . Accuracy of analytical–numerical solutions of the Michaelis–Menten equation. Comput. Appl. Math.. 2011;30:445-461.
[Google Scholar]
Gorder R.A.V., Vajravelu K., . On the selection of auxiliary functions, operators, and convergence control parameters in the application of the homotopy analysis method to nonlinear differential equations: a general approach. Commun. Nonlinear Sci. Numer. Simul.. 2009;14:4078-4089.
[Google Scholar]
He J.-H., . Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng.. 1999;178:257-262.
[Google Scholar]
He J.-H., . Comparison of homotopy perturbation method and homotopy analysis method. Appl. Math. Comput.. 2004;156:527-539.
[Google Scholar]
He J.-H., . An elementary introduction to the homotopy perturbation method. Comput. Math. Appl.. 2009;57:410-412.
[Google Scholar]
He J.-H., . Notes on the optimal variational iteration method. Appl. Math. Lett.. 2012;25:1579-1581.
[Google Scholar]
Hojjati M., Jafari S., . Semi-exact solution of elastic non-uniform thickness and density rotating disks by homotopy perturbation and Adomian’s decomposition methods. part i: Elastic solution. Int. J. Press. Vessels Pip.. 2008;85:871-878.
[Google Scholar]
Khader M., . On the numerical solutions for chemical kinetics system using Picard Padé technique. J. King Saud Univ. Eng. Sci. 2012
[CrossRef] [Google Scholar]
Khan Y., Vazquez-Leal H., Wu Q., . An efficient iterated method for mathematical biology model. Neural Comput. Appl. 2012:1-6.
[Google Scholar]
Khan Y., Wu Q., Faraz N., Yildirim A., . The effects of variable viscosity and thermal conductivity on a thin film flow over a shrinking/stretching sheet. Comput. Math. Appl.. 2011;61:3391-3399.
[Google Scholar]
Khan Y., Wu Q., Faraz N., Yildirim A., Madani M., . A new fractional analytical approach via a modified Riemann Liouville derivative. Appl. Math. Lett. 2011
[CrossRef] [Google Scholar]
Koak H., Yildirim A., Zhang D., Mohyud-Din S., . The comparative Boubaker polynomials expansion scheme (BPES) and homotopy perturbation method (HPM) for solving a standard nonlinear second-order boundary value problem. Math. Comput. Model.. 2011;54:417-422.
[Google Scholar]
Lal M., Moffatt D., . Picard’s successive approximation for non-linear two-point boundary-value problems. J. Comput. Appl. Math.. 1982;8:233-236.
[Google Scholar]
Layton W., Lenferink W., . Two-level Picard and modified Picard methods for the Navier–Stokes equations. Appl. Math. Comput.. 1995;69:263-274.
[Google Scholar]
Li J.-L., . Adomian’s decomposition method and homotopy perturbation method in solving nonlinear equations. J. Comput. Appl. Math.. 2009;228:168-173.
[Google Scholar]
Rajendran L., . Pad’e approximation for ECE and DISP processes at channel electrodes. Electrochem. Commun.. 2000;2:186-189.
[Google Scholar]
Sangaranarayanan M.V., Rajendran L., . Diffusion at ultramicroelectrodes: chronoamperometric current response using pad’e approximation. J. Phys. Chem. B. 1997;101:4583-4587.
[Google Scholar]
Nallasamy R., Rajendran L., . Chronoamperometric current at ultramicroelectrodes: Pad’e approximation for a reversible electron transfer scheme. Electroanalysis. 1998;10(7):506-511.
[Google Scholar]
Mastroberardino A., . Homotopy analysis method applied to electrohydrodynamic flow. Commun. Nonlinear Sci. Numer. Simul.. 2011;16:2730-2736.
[Google Scholar]
Merdan M., Gökdoğan A., Yildirim A., . On the numerical solution of the model for HIV infection of cd4⁺t cells. Comput. Math. Appl.. 2011;62:118-123.
[Google Scholar]
Noor M.A., Mohyud-Din S.T., . Variational iteration method for unsteady flow of gas through a porous medium using He’s polynomials and Padé approximants. Comput. Math. Appl.. 2009;58:2182-2189.
[CrossRef] [Google Scholar]
Odibat Z., Momani S., . The variational iteration method: an efficient scheme for handling fractional partial differential equations in fluid mechanics. Comput. Math. Appl.. 2009;58:2199-2208.
[Google Scholar]
Qian Y., Chen S., . Accurate approximate analytical solutions for multi-degree-of-freedom coupled Van der Pol–Duffing oscillators by homotopy analysis method. Commun. Nonlinear Sci. Numer. Simul.. 2010;15:3113-3130.
[Google Scholar]
Rach R., . On the Adomian decomposition method and comparisons with Picard’s method. J. Math. Anal. Appl.. 1987;128:480-483.
[Google Scholar]
Raftari B., Yildirim A., . Series solution of a nonlinear ODE arising in magnetohydrodynamic by HPM–Padé technique. Comput. Math. Appl.. 2011;61:1676-1681.
[Google Scholar]
Ramos J., . Picards iterative method for nonlinear advection–reaction–diffusion equations. Appl. Math. Comput.. 2009;215:1526-1536.
[Google Scholar]
Rashidi M.M., Dinarvand S., . Purely analytic approximate solutions for steady three-dimensional problem of condensation film on inclined rotating disk by homotopy analysis method. Nonlinear Anal. Real World Appl.. 2009;10:2346-2356.
[Google Scholar]
Saadati R., Dehghan M., Vaezpour S., Saravi M., . The convergence of He’s variational iteration method for solving integral equations. Comput. Math. Appl.. 2009;58:2167-2171.
[Google Scholar]
Safari M., Ganji D., Moslemi M., . Application of He’s variational iteration method and Adomian’s decomposition method to the fractional KdV–Burgers–Kuramoto equation. Comput. Math. Appl.. 2009;58:2091-2097.
[Google Scholar]
Shang X., Han D., . Application of the variational iteration method for solving nth-order integro-differential equations. J. Comput. Appl. Math.. 2010;234:1442-1447.
[Google Scholar]
Sheikholeslami M., Ashorynejad H., Ganji D., Yildirim A., . Homotopy perturbation method for three-dimensional problem of condensation film on inclined rotating disk. Sci. Iran.. 2012;19:437-442.
[Google Scholar]
Shukla A.K., Ramamohan T., Srinivas S., . Homotopy analysis method with a non-homogeneous term in the auxiliary linear operator. Commun. Nonlinear Sci. Numer. Simul.. 2012;17:3776-3787.
[Google Scholar]
Szinvelski C.R., Vilhena M.T., Carvalho J.C., Degrazia G.A., . Semi-analytical solution of the asymptotic Langevin Equation by the Picard Iterative Method. Environ. Model. Softw.. 2006;21:406-410.
[Google Scholar]
Tan Y., Abbasbandy S., . Homotopy analysis method for quadratic Riccati differential equation. Commun. Nonlinear Sci. Numer. Simul.. 2008;13:539-546.
[Google Scholar]
Turkyilmazoglu M., . An optimal variational iteration method. Appl. Math. Lett.. 2011;24:762-765.
[Google Scholar]
Vázquez-Leal H., Castañeda-Sheissa R., Filobello-Niño U., Sarmiento-Reyes A., Sánchez-Orea J., . High accurate simple approximation of normal distribution related integrals. Math. Problems Eng.. 2012;2012:22.
[Google Scholar]
Vazquez-Leal H., Filobello-Nino U., Castaneda-Sheissa R., Hernandez-Martinez L., Sarmiento-Reyes A., . Modified HPM’s inspired by homotopy continuation methods. Math. Problems Eng.. 2012;2012:19.
[Google Scholar]
Vazquez-Leal H., Filobello-Nino U., Yildirim A., Hernandez-Martinez L., Castaneda-Sheissa R., Sanchez-Orea J., Molinar-Solis J.E., Diaz-Sanchez A., . Transient and dc approximate expressions for diode circuits. IEICE Electr. Expr.. 2012;9:522-530.
[Google Scholar]
Wang Q., . The optimal homotopy-analysis method for Kawahara equation. Nonlinear Anal. Real World Appl.. 2011;12:1555-1561.
[Google Scholar]
Wang Y.-G., Lin W.-H., Liu N., . A homotopy perturbation-based method for large deflection of a cantilever beam under a terminal follower force. Int. J. Comput. Methods Eng. Sci. Mech.. 2012;13:197-201.
[Google Scholar]
Yildirim A., Koak H., . Homotopy perturbation method for solving the space time fractional advection dispersion equation. Adv. Water Resour.. 2009;32:1711-1716.
[Google Scholar]

Appendix A

Basic idea of HPM method

The basic idea of HPM method He (2004, 2009, 1999), Koak et al. (2011), Yildirim and Koak (2009), Vázquez-Leal et al. (2012), Vazquez-Leal et al. (2012a), Filobello-Nino et al. (2012b), Khan et al. (2011a), Faraz and Khan (2011), Khan et al. (2011b, 2012) is to introduce a homotopy parameter p, which takes values ranging from 0 up to 1. When parameter $p = 0$ , the equation usually reduces to a simple, or trivial, equation; then, p value is increased, gradually, up to one. The result is a sequence of deformations where every solution is closer to the last one. Eventually, at $p = 1$ , the homotopy equation is reduced to the original form of the equation and the final stage of deformation provides the desired solution. Generally, only few iterations are needed to achieve good accuracy.

For the HPM method, we consider that a nonlinear differential equation can be expressed as

(A.1)

A (u) - f (r) = 0, r \in Ω,

having as boundary condition

(A.2)

B (u, \frac{\partial u}{\partial η}) = 0, r \in Γ,

where L and N, are a linear and non-linear operators, respectively;

f (r)

is a known analytic function, B is a boundary operator, Γ is the boundary of domain Ω, and

\partial u / \partial η

denotes differentiation along the normal drawn outwards from Ω Wang et al. (2012). The operator A, generally, can be divided into the two operators, L and N, already described. Hence, (A.1) can be rewritten as

(A.3)

L (u) + N (u) - f (r) = 0 .

Generally, a homotopy can be expressed as

(A.4)

H (v, p) = (1 - p) [L (v) - L (u_{0})] + p (L (v) + N (v) - f (r)) = 0, p \in [0, 1] .

Also,

u_{0}

is the initial approximation to the solution of (A.3) that satisfies the boundary conditions, and p is known as the perturbation homotopy parameter. By analysing (A.4) we can conclude that

(A.5)

H (v, 0) = L (v) - L (u_{0}) = 0,

and

(A.6)

H (v, 1) = L (v) + N (v) - f (r) = 0 .

Assuming that the solution for (A.4) can be written as a power series of p

(A.7)

v = v_{0} + {pv}_{1} + p^{2} v_{2} + \dots .

When $p \to 1$ , the approximate solution for (A.1) is

(A.8)

u = \lim_{p \to 1} v = v_{0} + v_{1} + v_{2} + \dots .

The series (A.8) is convergent on most cases, nevertheless, convergence depends on the nonlinear operator $N (v)$ He (1999), Biazar and Aminikhah (2009), Biazar and Ghazvini (2009a).

A.1

Solution by HPM method

Using (A.4) and (17) we can establish the following homotopy equation

(A.9)

\begin{matrix} H (r, p) = (1 - p) (L (v) - L (u_{0})) \\ + p (v^{'} - \frac{1}{2} v + \frac{1}{4} v^{2} - \frac{1}{8} v^{3} + \frac{1}{16} v^{4} - \frac{1}{32} v^{5} + \frac{1}{64} v^{6}) = 0, \end{matrix}

where the linear operator is chosen as

(A.10)

L (v) = 2 v^{'} - 0.60691042571003 v .

Now, we choose as trial function the solution when $L (v) = 0$ , resulting

(A.11)

u_{0} = \exp (Cr),

where the adjustment parameter is chosen as

C = 0.303455212855015

Substituting (A.7) into (A.9), reordering and equating terms having the same p-powers, we obtain the following system of linear differential equations

(A.12)

\begin{matrix} 2 v_{1}^{'} - 2 {Cv}_{1} + \frac{1}{4} v_{0}^{2} - \frac{1}{2} v_{0} + 2 {Cv}_{0} - v_{0}^{'} - \frac{1}{32} v_{0}^{5} \\ - \frac{1}{8} v_{0}^{3} + \frac{1}{64} v_{0}^{6} + \frac{1}{16} v_{0}^{4} = 0, \\ v_{1} (0) = 0, \end{matrix}

(A.13)

\begin{matrix} 2 v_{2}^{'} - 2 {Cv}_{2} - \frac{5}{32} v_{0}^{4} v_{1} + \frac{1}{4} v_{0}^{3} v_{1} + 2 {Cv}_{1} - \frac{1}{2} v_{1} - v_{1}^{'} \\ + \frac{3}{32} v_{0}^{5} v_{1} - \frac{3}{8} v_{0}^{2} v_{1} + \frac{1}{2} v_{0} v_{1} = 0, \\ v_{2} (0) = 0, \end{matrix}

(A.14)

\begin{matrix} 2 v_{3}^{'} - \frac{1}{2} v_{2} + \frac{15}{64} v_{0}^{4} v_{1}^{2} - v_{2}^{'} - \frac{5}{32} v_{0}^{4} v_{2} + \frac{3}{8} v_{0}^{2} v_{1}^{2} + \frac{1}{2} v_{0} v_{2} + 2 {Cv}_{2} \\ - \frac{3}{8} v_{0}^{2} v_{2} + \frac{3}{32} v_{0}^{5} v_{2} - \frac{3}{8} v_{0} v_{1}^{2} + \frac{1}{4} v_{0}^{3} v_{2} - 2 {Cv}_{3} + \frac{1}{4} v_{1}^{2} - \frac{5}{16} v_{0}^{3} v_{1}^{2} = 0, \\ v_{3} (0) = 0, \end{matrix}

where the zero order approximation is

v_{0} = u_{0}

First order term is

(A.15)

v_{1} = - \frac{1}{3840 C} (\exp (Cr) (- 391 - 15 \exp (4 Cr) + 480 \exp (Cr) - 960 Cr + 1920 C^{2} r - 120 \exp (2 Cr) + 6 \exp (5 Cr) + 40 \exp (3 Cr))) .

Due to the complexity of exponential terms, (A.13) has no explicit closed-form solution. Therefore, HPM method failed and it is only possible to obtain the first order approximation.

The first order approximate solution for (14) is obtained using (A.8), giving as result

(A.16)

s (t) = \lim_{p \to 1} v = v_{0} + v_{1} .

Appendix B

Obtaining the optimal parameter C

We have used nonlinear fitting based on modified Newton method in order to find optimal parameter C that plays an important role for obtaining final series solution. We command from Maple software Release 15 and command convert with option rational, to set the adjustment parameters. In fact, the NonlinearFit command finds the given values of the parameters of the approximate model in such way that the sum of the squared k residuals is minimized. Also, in both cases HPM and NDHPM, functions $N (ν, p)$ and $f (r, p)$ can be expressed in terms of power series of p and provides solutions of equations in a simple way. Furthermore, we have perturbed the fractional term of Michaelis mention equation and we have approximated it by truncated Taylor series expansion and choosing suitable number of terms. Then, we separated the linear section and used non linear fitting method to find optimal value of C. Therefore, the second term of Lv is chosen in this way and naturally , it provides us the series of solutions after solving system of differential equations. This process will be repeated for the rest of the examples by means of HPM and NDHPM in this paper.

Introduction

Distribution of nonlinearities for HPM method (NDHPM)

Picard method and Padé aftertreatment

Padé approximants

Solution of Michaelis–Menten equation

Solution by NDHPM method
Solution by Picard–Padé method

Numerical illustration and discussion

Conclusions

Disclosure policy

Fulltext Views
6

PDF downloads
2

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Abbasbandy S., . Approximate solution for the nonlinear model of diffusion and reaction in porous catalysts by means of the homotopy analysis method. Chem. Eng. J.. 2008;136:144-150.
[Google Scholar]

[2] Abbasbandy S., . Homotopy analysis method for the Kawahara equation. Nonlinear Anal. Real World Appl.. 2010;11:307-312.
[Google Scholar]

[3] Abbasbandy S., Shivanian E., . Predictor homotopy analysis method and its application to some nonlinear problems. Commun. Nonlinear Sci. Numer. Simul.. 2011;16:2456-2468.
[Google Scholar]

[4] Abidi F., Omrani K., . The homotopy analysis method for solving the Fornberg Whitham equation and comparison with Adomianan’s decomposition method. Comput. Math. Appl.. 2010;59:2743-2750.
[Google Scholar]

[5] Altintan D., Ugur O., . Variational iteration method for SturmLiouville differential equations. Comput. Math. Appl.. 2009;58:322-328.
[Google Scholar]

[6] Baker G., . Essentials of Padé Approximations. New York: Academic Express; 1975.

[7] Bararnia H., Ghasemi E., Soleimani S., Ghotbi A.R., Ganji D., . Solution of the Falknerskan wedge flow by HPM Padé method. Adv. Eng. Softw.. 2012;43:44-52.
[CrossRef] [Google Scholar]

[8] Bataineh A.S., Noorani M., Hashim I., . On a new reliable modification of homotopy analysis method. Commun. Nonlinear Sci. Numer. Simul.. 2009;14:409-423.
[Google Scholar]

[9] Bellomo N., Sarafyan D., . On Adomian’s decomposition method and some comparisons with Picard’s iterative scheme. J. Math. Anal. Appl.. 1987;123:389-400.
[Google Scholar]

[10] Biazar J., Aminikhah H., . Study of convergence of homotopy perturbation method for systems of partial differential equations. Comput. Math. Appl.. 2009;58:2221-2230.
[Google Scholar]

[11] Biazar J., Ghazvini H., . Numerical solution for special non-linear Fredholm integral equation by HPM. Appl. Math. Comput.. 2008;195:681-687.
[Google Scholar]

[12] Biazar J., Ghazvini H., . Convergence of the homotopy perturbation method for partial differential equations. Nonlinear Anal. Real World Appl.. 2009;10:2633-2640.
[Google Scholar]

[13] Biazar J., Ghazvini H., . He’s homotopy perturbation method for solving systems of Volterra integral equations of the second kind. Chaos Solitons Fractals. 2009;39:770-777.
[Google Scholar]

[14] Chen X., Wang L., . The variational iteration method for solving a neutral functional–differential equation with proportional delays. Comput. Math. Appl.. 2010;59:2696-2702.
[Google Scholar]

[15] Chen Y., Liu J., . Homotopy analysis method for limit cycle flutter of airfoils. Appl. Math. Comput.. 2008;203:854-863.
[Google Scholar]

[16] El-Sayed A., Behiry S., Raslan W., . Adomian’s decomposition method for solving an intermediate fractional advection dispersion equation. Comput. Math. Appl.. 2010;59:1759-1765.
[Google Scholar]

[17] Ezzati R., Shakibi K., . Using Adomian’s decomposition and multiquadric quasi-interpolation methods for solving NewellWhitehead equation. Proc. Comput. Sci.. 2011;3:1043-1048.
[Google Scholar]

[18] Faraz N., Khan Y., . Analytical solution of electrically conducted rotating flow of a second grade fluid over a shrinking surface. Ain Shams Eng. J.. 2011;2:221-226.
[Google Scholar]

[19] Filobello-Nino U., Vazquez-Leal H., Khan Y., Castaneda-Sheissa R., Yildirim A., Hernandez-Martinez L., Sanchez-Orea J., Castaneda-Sheissa R., Bernal F.R., . HPM applied to solve nonlinear circuits: a study case. Appl. Math. Sci.. 2012;6:4331-4344.
[Google Scholar]

[20] Filobello-Nino U., Vazquez-Leal H., Castaneda-Sheissa R., Yildirim A., Hernandez-Martinez L., Pereyra-Diaz D., Perez-Sesma A., Hoyos-Reyes C., . An approximate solution of Blasius equation by using HPM method. Asian J. Math. Statist.. 2012;5:50-59.
[Google Scholar]

[21] Filobello-Nino U., Vazquez-Leal H., Khan Y., Pereyra-Diaz D., Perez-Sesma A., Diaz-Sanchez A., Jimenez-Fernandez V., Herrera-May A., Lopez-Martinez R., Sanchez-Orea J., . Nonlinearities distribution homotopy perturbation method as a tool to find power series solutions to differential equations. Nova Sci.. 2014;12:13-28.
[Google Scholar]

[22] Geng F., . A piecewise variational iteration method for treating a nonlinear oscillator of a mass attached to a stretched elastic wire. Comput. Math. Appl.. 2011;62:1641-1644.
[Google Scholar]

[23] Golinik M., . Explicit reformulations of time-dependent solution for a Michaelis Menten enzyme reaction model. Anal. Biochem.. 2010;406:94-96.
[Google Scholar]

[24] Golinik M., . Evaluation of enzyme kinetic parameters using explicit analytic approximations to the solution of the Michaelis Menten equation. Biochem. Eng. J.. 2011;53:234-238.
[Google Scholar]

[25] Gonzalez-Parra G., Acedo L., Arenas A., . Accuracy of analytical–numerical solutions of the Michaelis–Menten equation. Comput. Appl. Math.. 2011;30:445-461.
[Google Scholar]

[26] Gorder R.A.V., Vajravelu K., . On the selection of auxiliary functions, operators, and convergence control parameters in the application of the homotopy analysis method to nonlinear differential equations: a general approach. Commun. Nonlinear Sci. Numer. Simul.. 2009;14:4078-4089.
[Google Scholar]

[27] He J.-H., . Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng.. 1999;178:257-262.
[Google Scholar]

[28] He J.-H., . Comparison of homotopy perturbation method and homotopy analysis method. Appl. Math. Comput.. 2004;156:527-539.
[Google Scholar]

[29] He J.-H., . An elementary introduction to the homotopy perturbation method. Comput. Math. Appl.. 2009;57:410-412.
[Google Scholar]

[30] He J.-H., . Notes on the optimal variational iteration method. Appl. Math. Lett.. 2012;25:1579-1581.
[Google Scholar]

[31] Hojjati M., Jafari S., . Semi-exact solution of elastic non-uniform thickness and density rotating disks by homotopy perturbation and Adomian’s decomposition methods. part i: Elastic solution. Int. J. Press. Vessels Pip.. 2008;85:871-878.
[Google Scholar]

[32] Khader M., . On the numerical solutions for chemical kinetics system using Picard Padé technique. J. King Saud Univ. Eng. Sci. 2012
[CrossRef] [Google Scholar]

[33] Khan Y., Vazquez-Leal H., Wu Q., . An efficient iterated method for mathematical biology model. Neural Comput. Appl. 2012:1-6.
[Google Scholar]

[34] Khan Y., Wu Q., Faraz N., Yildirim A., . The effects of variable viscosity and thermal conductivity on a thin film flow over a shrinking/stretching sheet. Comput. Math. Appl.. 2011;61:3391-3399.
[Google Scholar]

[35] Khan Y., Wu Q., Faraz N., Yildirim A., Madani M., . A new fractional analytical approach via a modified Riemann Liouville derivative. Appl. Math. Lett. 2011
[CrossRef] [Google Scholar]

[36] Koak H., Yildirim A., Zhang D., Mohyud-Din S., . The comparative Boubaker polynomials expansion scheme (BPES) and homotopy perturbation method (HPM) for solving a standard nonlinear second-order boundary value problem. Math. Comput. Model.. 2011;54:417-422.
[Google Scholar]

[37] Lal M., Moffatt D., . Picard’s successive approximation for non-linear two-point boundary-value problems. J. Comput. Appl. Math.. 1982;8:233-236.
[Google Scholar]

[38] Layton W., Lenferink W., . Two-level Picard and modified Picard methods for the Navier–Stokes equations. Appl. Math. Comput.. 1995;69:263-274.
[Google Scholar]

[39] Li J.-L., . Adomian’s decomposition method and homotopy perturbation method in solving nonlinear equations. J. Comput. Appl. Math.. 2009;228:168-173.
[Google Scholar]

[40] Rajendran L., . Pad’e approximation for ECE and DISP processes at channel electrodes. Electrochem. Commun.. 2000;2:186-189.
[Google Scholar]

[41] Sangaranarayanan M.V., Rajendran L., . Diffusion at ultramicroelectrodes: chronoamperometric current response using pad’e approximation. J. Phys. Chem. B. 1997;101:4583-4587.
[Google Scholar]

[42] Nallasamy R., Rajendran L., . Chronoamperometric current at ultramicroelectrodes: Pad’e approximation for a reversible electron transfer scheme. Electroanalysis. 1998;10(7):506-511.
[Google Scholar]

[43] Mastroberardino A., . Homotopy analysis method applied to electrohydrodynamic flow. Commun. Nonlinear Sci. Numer. Simul.. 2011;16:2730-2736.
[Google Scholar]

[44] Merdan M., Gökdoğan A., Yildirim A., . On the numerical solution of the model for HIV infection of cd4⁺t cells. Comput. Math. Appl.. 2011;62:118-123.
[Google Scholar]

[45] Noor M.A., Mohyud-Din S.T., . Variational iteration method for unsteady flow of gas through a porous medium using He’s polynomials and Padé approximants. Comput. Math. Appl.. 2009;58:2182-2189.
[CrossRef] [Google Scholar]

[46] Odibat Z., Momani S., . The variational iteration method: an efficient scheme for handling fractional partial differential equations in fluid mechanics. Comput. Math. Appl.. 2009;58:2199-2208.
[Google Scholar]

[47] Qian Y., Chen S., . Accurate approximate analytical solutions for multi-degree-of-freedom coupled Van der Pol–Duffing oscillators by homotopy analysis method. Commun. Nonlinear Sci. Numer. Simul.. 2010;15:3113-3130.
[Google Scholar]

[48] Rach R., . On the Adomian decomposition method and comparisons with Picard’s method. J. Math. Anal. Appl.. 1987;128:480-483.
[Google Scholar]

[49] Raftari B., Yildirim A., . Series solution of a nonlinear ODE arising in magnetohydrodynamic by HPM–Padé technique. Comput. Math. Appl.. 2011;61:1676-1681.
[Google Scholar]

[50] Ramos J., . Picards iterative method for nonlinear advection–reaction–diffusion equations. Appl. Math. Comput.. 2009;215:1526-1536.
[Google Scholar]

[51] Rashidi M.M., Dinarvand S., . Purely analytic approximate solutions for steady three-dimensional problem of condensation film on inclined rotating disk by homotopy analysis method. Nonlinear Anal. Real World Appl.. 2009;10:2346-2356.
[Google Scholar]

[52] Saadati R., Dehghan M., Vaezpour S., Saravi M., . The convergence of He’s variational iteration method for solving integral equations. Comput. Math. Appl.. 2009;58:2167-2171.
[Google Scholar]

[53] Safari M., Ganji D., Moslemi M., . Application of He’s variational iteration method and Adomian’s decomposition method to the fractional KdV–Burgers–Kuramoto equation. Comput. Math. Appl.. 2009;58:2091-2097.
[Google Scholar]

[54] Shang X., Han D., . Application of the variational iteration method for solving nth-order integro-differential equations. J. Comput. Appl. Math.. 2010;234:1442-1447.
[Google Scholar]

[55] Sheikholeslami M., Ashorynejad H., Ganji D., Yildirim A., . Homotopy perturbation method for three-dimensional problem of condensation film on inclined rotating disk. Sci. Iran.. 2012;19:437-442.
[Google Scholar]

[56] Shukla A.K., Ramamohan T., Srinivas S., . Homotopy analysis method with a non-homogeneous term in the auxiliary linear operator. Commun. Nonlinear Sci. Numer. Simul.. 2012;17:3776-3787.
[Google Scholar]

[57] Szinvelski C.R., Vilhena M.T., Carvalho J.C., Degrazia G.A., . Semi-analytical solution of the asymptotic Langevin Equation by the Picard Iterative Method. Environ. Model. Softw.. 2006;21:406-410.
[Google Scholar]

[58] Tan Y., Abbasbandy S., . Homotopy analysis method for quadratic Riccati differential equation. Commun. Nonlinear Sci. Numer. Simul.. 2008;13:539-546.
[Google Scholar]

[59] Turkyilmazoglu M., . An optimal variational iteration method. Appl. Math. Lett.. 2011;24:762-765.
[Google Scholar]

[60] Vázquez-Leal H., Castañeda-Sheissa R., Filobello-Niño U., Sarmiento-Reyes A., Sánchez-Orea J., . High accurate simple approximation of normal distribution related integrals. Math. Problems Eng.. 2012;2012:22.
[Google Scholar]

[61] Vazquez-Leal H., Filobello-Nino U., Castaneda-Sheissa R., Hernandez-Martinez L., Sarmiento-Reyes A., . Modified HPM’s inspired by homotopy continuation methods. Math. Problems Eng.. 2012;2012:19.
[Google Scholar]

[62] Vazquez-Leal H., Filobello-Nino U., Yildirim A., Hernandez-Martinez L., Castaneda-Sheissa R., Sanchez-Orea J., Molinar-Solis J.E., Diaz-Sanchez A., . Transient and dc approximate expressions for diode circuits. IEICE Electr. Expr.. 2012;9:522-530.
[Google Scholar]

[63] Wang Q., . The optimal homotopy-analysis method for Kawahara equation. Nonlinear Anal. Real World Appl.. 2011;12:1555-1561.
[Google Scholar]

[64] Wang Y.-G., Lin W.-H., Liu N., . A homotopy perturbation-based method for large deflection of a cantilever beam under a terminal follower force. Int. J. Comput. Methods Eng. Sci. Mech.. 2012;13:197-201.
[Google Scholar]

[65] Yildirim A., Koak H., . Homotopy perturbation method for solving the space time fractional advection dispersion equation. Adv. Water Resour.. 2009;32:1711-1716.
[Google Scholar]