Solving the interaction of electromagnetic wave with electron by VIM

M. Matinfar; S. Mirzanezhad; M. Ghasemi; M. Salehi

doi:10.1016/j.jksus.2014.03.001

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original article

27 (

); 63-70

doi:

10.1016/j.jksus.2014.03.001

Solving the interaction of electromagnetic wave with electron by VIM

M. Matinfar^{^a,*}, S. Mirzanezhad^{^b}, M. Ghasemi^{^a}, M. Salehi^{^b}

a Department of Mathematics, University of Mazandaran, P.O. Box 47415-95447, Babolsar, Iran

b Department of Physics, University of Mazandaran, P.O. Box 47415-95447, Babolsar, Iran

*Corresponding author. Tel.: +98 1125342430; fax: +98 1125342460 m.matinfar@umz.ac.ir (M. Matinfar)

Received: 2014-1-23, Accepted: 2014-3-29, Published: 2014-01-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Available online 12 April 2014

Peer review under responsibility of King Saud University.

Abstract

In this paper the interaction of electromagnetic wave with electron is studied by Variational Iteration Method. This phenomenon is very important in physics and one of its application is, generating the High-Order Harmonics from plasma surface. Obtained results are in excellent agreement with experimental results and show the efficiency of applied technique.

Keywords

Variational Iteration Method

Harmonic generation

Oscillating mirror

Show Related Articles from PubMed

1 Introduction

One of the most important applications of differential equations is modeling the phenomena that happen in the nature. But the non-linear part that exists in most of these equations makes it difficult to obtain the exact solution and finding an appropriate method that gives the best approximation is a very big challenge. In recent decades, numerical calculation methods are good means of analyzing these equations. But in the numerical techniques, besides the volume of computational work, stability and convergence should be considered in order to avoid divergent or inappropriate results. So, these techniques cannot be used in a wide class of differential equations and it seems using some analytical techniques such as Homotopy Perturbation Method (HPM) (Rajeev and Kushwaha, 2013; Ebadian and Dastani, 2012; Sheikholeslami et al., 2012a ), Adomian Decomposition Method (ADM) (Wazwaz et al., 2013; Gharsseldien and Hemida, 2009; Sheikholeslami et al., 2012a,b, 2013 ) Variational Iteration Method Using He’s Polynomials (VIMHP) (Matinfar and Ghasemi, 2010, Matinfar and Ghasemi, 2013) can end the problems that arise in solving procedures. One of the most important phenomena in nonlinear optics is generating harmonics of the highest possible order. As we know nonlinear optical processes become more efficient at higher laser intensities, but in some cases the best quality of changes in the nature of the nonlinearity of the laser–matter interaction can be seen in certain characteristic intensity regimes (Voitiv and Ullrich, 2001; Voitiv et al., 2002).

Harmonic generation by an intense light wave incident on a plasma-vacuum boundary involves a very complex and collective interaction of the electrons with the electromagnetic field and can be investigated by oscillating mirror model. Oscillating mirror approximation (Voitiv et al., 2005; Dorner et al., 2000; Ullrich et al., 2003; Moshammer et al., 1996) consists of two distinct steps: in the first step the details of the electron spatial distribution are ignored and the collective electronic motion is represented by the motion of some characteristic electronic boundary, e.g., the critical density surface. This surface represents the oscillating mirror from which the incident light is reflected with the notification of having fixed ions. In the second step, the emission from the moving boundary is calculated, in particular the harmonic spectrum that is generated upon reflection of the incident light.

As we know, the over dense plasma is highly reflective and we have both electric and magnetic fields due to the incident and reflected waves. Therefore, the electrons near the plasma boundary should be driven from both fields. It is in the case that inside the plasma, the electromagnetic fields decay exponentially over a distance given by the skin depth. The motion equation of an electron near the boundary is

(1)

m \frac{d^{2} \vec{r}}{{dt}^{2}} = - e \vec{E_{1}} - e \vec{E} - e \vec{V} \times \vec{B} = {\vec{F}}_{p} + {\vec{F}}_{em},

where

E_{1}

is the longitudinal electric field and resulted from the electron-ion charge separation. The light with the electronic and magnetic field strengths of E and B is acting on the electron with force

F_{em}

. A qualitative picture of the motion can be obtained by considering the orbit of a single free electron under the action of the electromagnetic wave of frequency

w_{0}

, and neglecting restoring force

F_{p}

(Corkum, 1993; Brabec, 2008).

This paper is advocated to investigate this phenomenon by the Variational Iteration Method (VIM). The rest of this paper is organized as follows: Section 2 describes the details of the proposed method. Section 3 indicates sufficient conditions for convergence of applied technique. Section 4 explains related partial differential equations which interaction of electromagnetic wave with electron are obtained from and solving procedure. Section 5 shows the simulation results. Finally, conclusions are presented in Section 6.

2 Variational Iteration Method

The Variational Iteration Method, which provides an analytical approximate solution, is applied to various nonlinear problems (Biazar et al., 2010; Ganji et al., 2009; Gholami and Ghambari, 2011; Hassan and Alotaibi, 2010; Khader, 2013; Kafash et al., 2013). In this section, we present a brief description of VIM. This approach can be implemented, in a reliable and efficient way, to handle the following nonlinear differential equation

(2)

L [u (r)] + N [u (r)] = g (r), r > 0,

where

L = \frac{d^{m}}{{dr}^{m}}, m \in N

, is a linear operator, N is a nonlinear operator and

g (r)

is the source inhomogeneous term, subject to the initial conditions

(3)

u^{(k)} (0) = c_{k}, k = 0, 1, 2, \dots, m - 1 .

where

c_{k}

is a real number. According to the He’s Variational Iteration Method, we can construct a correction functional for Eq. (2) as follows:

u_{i + 1} (r) = u_{i} (r) + \int_{0}^{r} λ (τ) \{{Lu}_{i} (τ) + N \tilde{u_{i}} (τ) - g (τ)\} d τ, i ⩾ 0,

where

λ (τ)

is a general Lagrangian multiplier and can be identified optimally via variational theory. As we can see, because of the existence of nonlinear part in Eq. (2), it is not possible to find the optimal value of Lagrange multiplier exactly. But we can find an approximation of that by considering a restriction on nonlinear part that causes this part to be ignored in procedure for calculating

λ (τ)

and is denoted by

\tilde{u_{i}}

. The restriction that is mentioned is having restricted variation i.e.

δ {\tilde{u}}_{i} = 0

. Making the above functional stationary with

δ \tilde{u_{i}} = 0

δ u_{i + 1} (r) = δ u_{i} (r) + δ \int_{0}^{r} λ (τ) \{{Lu}_{i} (τ) - g (τ)\} d τ,

yields the following Lagrange multipliers,

(4)

\{\begin{matrix} λ = - 1 & for m = 1, \\ λ = τ - r, & for m = 2, \end{matrix}

and in general,

λ = \frac{{(- 1)}^{m}}{(m - 1)!} {(τ - r)}^{(m - 1)}, for m ⩾ 1 .

The successive approximations $u_{i} (r), i ⩾ 0$ of the solution $u (r)$ will be readily obtained upon using the obtained Lagrange multiplier and by using selective function $u_{0}$ which satisfies initial conditions. In our alternative approach we can select the initial approximation $u_{0}$ as

(5)

u_{0} = \sum_{k = 0}^{m - 1} \frac{c_{k}}{k!} r^{k} .

Consequently, the exact solution may be obtained as follows $u (r) = \lim_{i \to \infty} u_{i} (r) .$

3 Convergence analysis

In order to study the convergence of the Variational Iteration Method, according to the approach of VIM presented in the previous section, consider the following equation:

(6)

L [u (r)] + N [u (r)] = g (r) .

Based on what illustrated above, the optimal value of Lagrange multiplier in general case can be found as: $λ = \frac{{(- 1)}^{m}}{(m - 1)!} {(τ - r)}^{(m - 1)}, for m ⩾ 1 .$

So, we have $u_{n + 1} (r) = u_{n} (r) + \int_{0}^{r} \frac{{(- 1)}^{m}}{(m - 1)!} {(τ - r)}^{(m - 1)} \{L [u (τ)] + N [u (τ)] - g (τ)\} d τ .$

Now, define the operator $A [u]$ as

(7)

A [u] = \int_{0}^{r} \frac{{(- 1)}^{m}}{(m - 1)!} {(τ - r)}^{(m - 1)} \{L [u (τ)] + N [u (τ)] - g (τ)\} d τ,

and components

v_{k}, k = 0, 1, 2, \dots

, as

(8)

\{\begin{matrix} v_{0} = u_{0}, \\ v_{1} = A [v_{0}], \\ v_{2} = A [v_{0} + v_{1}], \\ ⋮ \\ v_{k + 1} = A [v_{0} + v_{1} + v_{2} + \dots + v_{k}] . \end{matrix}

we have:

(9)

u (r) = \lim_{k \to \infty} u_{k} (r) = \sum_{k = 0}^{+ \infty} v_{k} .

Therefore, using (7) and (8) the solution of Eq. (2) can be obtained as follows $u (r) = \sum_{k = 0}^{+ \infty} v_{k} (r) .$

3.1

3.1 Convergence theorem

Theorem 3.1

Let A, defined in (7), be an operator from a Hilbert space H to H. The series solution $u = \sum_{k = 0}^{+ \infty} v_{k}$ defined in (9) converges if $\exists 0 < γ < 1$ such that $‖v_{k + 1}‖ ⩽ γ ‖v_{k}‖$ , for some $k \in N \cup \{0\}$

Theorem (3.1) is a special case of Banach’s fixed point theorem. In what follows we briefly give the proof of Theorem (3.1).

proof

Define the sequence ${\{s_{n}\}}_{n = 0}^{+ \infty}$ as, $\{\begin{matrix} s_{0} = v_{0}, \\ s_{1} = v_{0} + v_{1}, \\ s_{2} = v_{0} + v_{1} + v_{2}, \\ ⋮ \\ s_{n} = v_{0} + v_{1} + v_{2} + \dots + v_{n}, \end{matrix}$ and we show that ${\{s_{n}\}}_{n = 0}^{+ \infty}$ is a Cauchy sequence in the Hilbert space H. For this purpose, consider $‖s_{n + 1} - s_{n}‖ = ‖v_{n + 1}‖ ⩽ γ ‖v_{n}‖ ⩽ γ^{2} ‖v_{n - 1}‖ ⩽ \dots γ^{n + 1} ‖v_{0}‖,$

For every $n, j \in N, n ⩾ j$ , we have, $\begin{matrix} ‖s_{n} - s_{j}‖ = ‖(s_{n} - s_{n - 1}) + (s_{n - 1} - s_{n - 2}) + \dots + (s_{j + 1} - s_{j})‖ \\ ⩽ ‖(s_{n} - s_{n - 1})‖ + ‖(s_{n - 1} - s_{n - 2})‖ + \dots + ‖(s_{j + 1} - s_{j})‖ \\ ⩽ γ^{n} ‖v_{0}‖ + γ^{n - 1} ‖v_{0}‖ + \dots + γ^{j + 1} ‖v_{0}‖ \\ = \frac{1 - γ^{n - j}}{1 - γ} γ^{j + 1} ‖v_{0}‖, \end{matrix}$ and since $0 < γ < 1$ we get, $\lim_{n, j \to + \infty} ‖s_{n} - s_{j}‖ = 0 .$

Therefore, ${\{s_{n}\}}_{n = 0}^{+ \infty}$ is a Cauchy sequence in the Hilbert space H and it implies that the series solution $u = \sum_{k = 0}^{+ \infty} v_{k}$ defined in (9), converges. This completes the proof of Theorem (3.1). □

3.2

3.2 Uniqueness theorem

Theorem 3.2

If the series solution $u = \sum_{k = 0}^{+ \infty} v_{k}$ , defined in (9) converges, then it is an exact solution of the nonlinear problem (2).

proof

Suppose the series solution (9) converges, say $φ (r) = \sum_{k = 0}^{+ \infty} v_{k}$ , then we have

(10)

\lim_{j \to \infty} v_{j} = 0,

(11)

\sum_{j = 0}^{n} [v_{j + 1} - v_{j}] = v_{n + 1} - v_{0},

and so,

(12)

\sum_{j = 0}^{\infty} [v_{j + 1} - v_{j}] = \lim_{j \to \infty} v_{j} - v_{0} = - v_{0} .

Applying the operator $L = \frac{d^{m}}{{dr}^{m}}, m \in N$ to both sides of Eq. (12) then, from (5), we obtain

(13)

\sum_{j = 0}^{\infty} L [v_{j + 1} - v_{j}] = - L [v_{0}] = 0 .

On the other hand, from definition (8), we have

(14)

L [v_{j + 1} - v_{j}] = - L [A [v_{0} + v_{1} + \dots + v_{j}] - A [v_{0} + v_{1} + \dots + v_{j - 1}]]

when

j ⩾ 1

and so, using definition (7) we get

(15)

L [v_{j + 1} - v_{j}] = L \{\int_{0}^{r} \frac{{(- 1)}^{m}}{(m - 1)!} {(τ - r)}^{(m - 1)} {L [v_{0} + \dots + v_{j}] - L [v_{0} + \dots + v_{j - 1}] + N [v_{0} + \dots + v_{j}] - N [v_{0} + \dots + v_{j - 1}]\} d τ, j ⩾ 1 .

Now, the operator $A [u]$ gives the mth-fold integral of $Lu (r) + Nu (r) - g (r)$ . Since, the differential operator $L = \frac{d^{m}}{{dr}^{m}}$ of order m is left inverse to mth-fold integral operator, the Eq. (15) becomes as

(16)

L [v_{j + 1} - v_{j}] = L [v_{j}] + N [v_{0} + v_{1} + \dots + v_{j}] - N [v_{0} + v_{1} + \dots + v_{j - 1}], j ⩾ 1 .

Consequently, we have

(17)

\begin{matrix} \sum_{j = 0}^{n} L [v_{j + 1} - v_{j}] = L [v_{0}] + N [v_{0}] - g (t) \\ + L [v_{1}] + N [v_{0} + v_{1}] - N [v_{0}] \\ ⋮ \\ + L [v_{n}] + N [v_{0} + \dots + v_{n}] - N [v_{0} + \dots + v_{n - 1}] . \end{matrix}

Therefore,

(18)

\sum_{j = 0}^{\infty} L [v_{j + 1} - v_{j}] = L [\sum_{j = 0}^{\infty} v_{j}] + N [\sum_{j = 0}^{\infty} v_{j}] - g (r) .

From (13) and (18), we can observe that $φ (r) = \sum_{j = 0}^{\infty} v_{j}$ is the solution of Eq. (2) and this completes the proof of Theorem 3.2. □

4 Calculation

To illustrate the proposed method for solving the equation that is related to the generation of High Order Harmonics, three cases are considered. Note that in interaction of ultra intense radiation with plasma, $F_{p}$ can be ignored in Eq. (1), Brabec, 2008). So, we have

(19)

m \frac{d^{2} \vec{r}}{{dt}^{2}} = - e (\vec{E} + \vec{V} \times \vec{B}) .

Case I:

In this case we study the interaction of electromagnetic wave with single-color s-polarization. Therefore, we can choose

(20)

\{\begin{matrix} \vec{E} = E_{0} Cos (wt) \hat{j}, \\ \vec{B} = B_{0} Cos (wt) \hat{k} . \end{matrix}

So, electromagnetic wave moves along x-axis. Substituting Eq. (20) in Eq. (1) yields:

(21)

\{\begin{matrix} m \ddot{x} = - {ev}_{y} B_{0} Cos (wt), \\ m \ddot{y} = - e (E_{0} Cos (wt) - v_{x} B_{0} Cos (wt)), \\ m \ddot{z} = 0 . \end{matrix}

Solving third equation in (21) results $\dot{z} = cte$ , then we do not have any oscillation along z-axis. Using $B_{0} = \frac{E_{0}}{c}$ that is obtained by the Maxwell equation gives:

(22)

\{\begin{matrix} \ddot{x} = - \frac{e}{m} \frac{E_{0}}{c} Cos (wt) \dot{y}, \\ \ddot{y} = - \frac{e}{m} E_{0} Cos (wt) + \frac{e}{m} \frac{E_{0}}{c} Cos (wt) \dot{x} . \end{matrix}

By substituting

(23)

\{\begin{matrix} x = \frac{xw}{c}, \\ E = \frac{eE}{mwc}, \\ y = \frac{yw}{c}, \\ t = wt, \end{matrix}

we have following dimensionless equations:

(24)

\{\begin{matrix} \ddot{x} = - E_{0} Cos (t) \dot{y}, \\ \ddot{y} = - E_{0} Cos (t) + E_{0} Cos (t) \dot{x} . \end{matrix}

To solve Eq. (24) by VIM, we should first construct the correction functional as follows $\{\begin{matrix} x_{n + 1} (t) = x_{n} (t) + \int_{0}^{t} λ_{1} (τ) {x_{n_{τ τ}} + E_{0} Cos (τ) {\tilde{\dot{y}}}_{n}} d τ, \\ y_{n + 1} (t) = y_{n} (t) + \int_{0}^{t} λ_{2} (τ) {y_{n_{τ τ}} - E_{0} Cos (τ) {\tilde{\dot{x}}}_{n} + E_{0} Cos (τ)} d τ, \end{matrix}$ where ${\tilde{\dot{x}}}_{n}$ and ${\tilde{\dot{y}}}_{n}$ are considered as restricted variations, i.e. $δ {\tilde{\dot{x}}}_{n} = δ {\tilde{\dot{y}}}_{n} = 0$ .

To find the optimal value of $λ_{1} (τ)$ and $λ_{2} (τ)$ , we have $\{\begin{matrix} δ x_{n + 1} (t) = δ x_{n} (t) + δ \int_{0}^{t} λ_{1} (τ) {x_{n_{τ τ}} + E_{0} Cos (τ) {\tilde{\dot{y}}}_{n}} d τ, \\ δ y_{n + 1} (t) = δ y_{n} (t) + δ \int_{0}^{t} λ_{2} (τ) {y_{n_{τ τ}} - E_{0} Cos (τ) {\tilde{\dot{x}}}_{n} + E_{0} Cos (τ)} d τ, \end{matrix}$ or $\{\begin{matrix} δ x_{n + 1} (t) = δ x_{n} (t) + \int_{0}^{t} λ_{1} (τ) {δ x_{n_{τ τ}}} d τ, \\ δ y_{n + 1} (t) = δ y_{n} (t) + \int_{0}^{t} λ_{2} (τ) {δ y_{n_{τ τ}}} d τ, \end{matrix}$ which results

(25)

δ x_{n + 1} (t) = δ x_{n} (t) + λ_{1} (τ) δ x_{n_{τ}} |_{τ = t} - λ_{1}^{'} (τ) δ x_{n} |_{τ = t} + \int_{0}^{t} λ_{1}^{″} (τ) δ x_{n} d τ,

(26)

δ y_{n + 1} (t) = δ y_{n} (t) + λ_{2} (τ) δ y_{n_{τ}} |_{τ = t} - λ_{2}^{'} (τ) δ y_{n} |_{τ = t} + \int_{0}^{t} λ_{2}^{″} (τ) δ y_{n} d τ .

Therefore, the stationary conditions are obtained in the following forms

(27)

\{\begin{matrix} λ_{1} (τ) |_{τ = t} = 0, \\ 1 - λ_{1}^{'} (τ) |_{τ = t} = 0, \\ λ_{1}^{″} (τ) |_{τ = t} = 0, \end{matrix}

and

(28)

\{\begin{matrix} λ_{2} (τ) |_{τ = t} = 0, \\ 1 - λ_{2}^{'} (τ) |_{τ = t} = 0, \\ λ_{2}^{″} (τ) |_{τ = t} = 0, \end{matrix}

which results

λ_{1} (τ) = λ_{2} (τ) = τ - t

Therefore, the variational iteration formula can be written as follows $\{\begin{matrix} x_{n + 1} (t) = x_{n} (t) + \int_{0}^{t} (τ - t) {x_{n_{τ τ}} + E_{0} Cos (τ) {\dot{y}}_{n}} d τ, \\ y_{n + 1} (t) = y_{n} (t) + \int_{0}^{t} (τ - t) {y_{n_{τ τ}} - E_{0} Cos (τ) {\dot{x}}_{n} + E_{0} Cos (τ)} d τ, \end{matrix}$

It is clear that one form of (24) solutions is $(Sin)$ or $(Cos)$ or expansion of them. So, we can choose $x_{0} = - . 07 t$ and $y_{0} = . 01 Cos (t)$ as initial approximations, and other components can be obtained as follows

(29)

\begin{matrix} x_{1} (t) = x_{0} (t) + \int_{0}^{t} (τ - t) {x_{0_{τ τ}} + E_{0} Cos (τ) {\dot{y}}_{0}} d τ \\ = - \frac{11}{60} t - \frac{1}{800} Cos (t) Sin (t), \\ x_{2} (t) = x_{1} (t) + \int_{0}^{t} (τ - t) {x_{1_{τ τ}} + E_{0} Cos (τ) {\dot{y}}_{1}} d τ \\ = - \frac{1}{320} t - \frac{107}{1600} Cos (t) Sin (t), \\ x_{3} (t) = x_{2} (t) + \int_{0}^{t} (τ - t) {x_{2_{τ τ}} + E_{0} Cos (τ) {\dot{y}}_{2}} d τ \\ = - \frac{161}{51200} t - (\frac{15401}{230400} + \frac{1}{92, 160} {Cos}^{2} (t) - \frac{1}{460800} {Sin}^{2} (t)) \\ \times Sin (t) Cos (t), \\ ⋮ \end{matrix}

And

(30)

\begin{matrix} y_{1} (t) = y_{0} (t) + \int_{0}^{t} (τ - t) {y_{0_{τ τ}} - E_{0} Cos (τ) {\dot{x}}_{0} + E_{0} Cos (τ)} d τ \\ = - \frac{21}{40} + \frac{107}{200} Cos (t), \\ y_{2} (t) = y_{1} (t) + \int_{0}^{t} (τ - t) {y_{1_{τ τ}} - E_{0} Cos (τ) {\dot{x}}_{1} + E_{0} Cos (τ)} d τ \\ = - \frac{1889}{3600} + (\frac{133849}{259200} - \frac{1}{14400} {Sin}^{2} (t) + \frac{1}{14400} {Cos}^{2} (t)) Cos (t), \\ y_{3} (t) = y_{2} (t) + \int_{0}^{t} (τ - t) {y_{2_{τ τ}} - E_{0} Cos (τ) {\dot{x}}_{2} + E_{0} Cos (τ)} d τ, \\ = - \frac{3673}{7200} + (\frac{133849}{259200} - \frac{191}{51840} {Sin}^{2} (t) + \frac{971}{259200} {Cos}^{2} (t)) Cos (t), \\ ⋮ \end{matrix}

and the solution will be

(31)

\{\begin{matrix} x (t) = \lim_{i \to \infty} x_{i} (t), \\ y (t) = \lim_{i \to \infty} y_{i} (t) . \end{matrix}

Note that the solutions are obtained at $E_{0} = . 5$ .

Case II:

In this case the interaction of electromagnetic wave with two-color, parallel polarization with the same amplitude is investigated. Therefore,

(32)

\{\begin{matrix} \vec{E} = E_{0} (Cos (w_{1} t) + Cos (w_{2} t)) \hat{j}, \\ \vec{B} = B_{0} (Cos (w_{1} t) + Cos (w_{2} t)) \hat{k} . \end{matrix}

Substituting Eq. (32) in Eq. (1) yields:

(33)

\{\begin{matrix} m \ddot{x} = - {ev}_{y} B_{0} (Cos (w_{1} t) + Cos (w_{2} t)), \\ m \ddot{y} = - e (E_{0} - v_{x} B_{0}) (Cos (w_{1} t) + Cos (w_{2} t)), \\ m \ddot{z} = 0 . \end{matrix}

It is clear that solving third equation in (33) results $\dot{z} = cte$ , then we do not have any oscillation along z-axis. As the same as previous case we have following dimensionless equations:

(34)

\{\begin{matrix} \ddot{x} = - E_{0} (Cos (t) + Cos (\frac{w_{2}}{w_{1}} t)) \dot{y}, \\ \ddot{y} = - E_{0} (Cos (t) + Cos (\frac{w_{2}}{w_{1}} t)) + E_{0} (Cos (t) + Cos (\frac{w_{2}}{w_{1}} t)) \dot{x} . \end{matrix}

To solve Eq. (34) by VIM, we should first construct the correction functional and determine the best value of Lagrange multiplier. As stated and done in the previous case we have $λ_{1} (τ) = λ_{2} (τ) = τ - t$ .

So, the variational iteration formula can be written as follows

(35)

\begin{matrix} x_{n + 1} (t) = x_{n} (t) + \int_{0}^{t} (τ - t) {x_{n_{τ τ}} + E_{0} (Cos (τ) + Cos (\frac{w_{2}}{w_{1}} τ)) {\dot{y}}_{n}} d τ, \\ y_{n + 1} (t) = y_{n} (t) + \int_{0}^{t} (τ - t) \{y_{n_{τ τ}} - E_{0} (Cos (τ) + Cos (\frac{w_{2}}{w_{1}} τ)) {\dot{x}}_{n} \\ + E_{0} (Cos (τ) + Cos (\frac{w_{2}}{w_{1}} τ))\} d τ, \end{matrix}

Using $x_{0} = - 0.08 t$ and $y_{0} = . 01 Cos (t)$ as initial approximations, the other components of solutions can be obtained as follows:

(36)

\begin{matrix} x_{1} (t) = x_{0} (t) + \int_{0}^{t} (τ - t) \{x_{0_{τ τ}} + E_{0} (Cos (τ) + Cos (\frac{w_{2}}{w_{1}} τ)) {\dot{y}}_{0}\} d τ \\ = - \frac{193}{2400} t + \frac{1}{400} Sin (t) - \frac{1}{1600} Sin (2 t) \\ - \frac{1}{3600} Sin (3 t), \\ x_{2} (t) = x_{1} (t) + \int_{0}^{t} (τ - t) \{x_{1_{τ τ}} + E_{0} (Cos (τ) + Cos (\frac{w_{2}}{w_{1}} τ)) {\dot{y}}_{1}\} d τ \\ = \frac{7}{1600} t + \frac{27}{400} Sin (t) - \frac{27}{800} Sin (2 t) \\ - \frac{9}{400} Sin (3 t) - \frac{27}{6400} Sin (4 t), \\ ⋮ \end{matrix}

And

(37)

\begin{matrix} y_{1} (t) = y_{0} (t) + \int_{0}^{t} (τ - t) \{y_{0_{τ τ}} - E_{0} (Cos (τ) + Cos (\frac{w_{2}}{w_{1}} τ)) {\dot{x}}_{0} \\ + E_{0} (Cos (τ) + Cos (\frac{w_{2}}{w_{1}} τ))\} d τ \\ = - \frac{133}{200} + \frac{27}{50} Cos (t) + \frac{27}{200} Cos (2 t), \\ y_{2} (t) = y_{1} (t) + \int_{0}^{t} (τ - t) \{y_{1_{τ τ}} - E_{0} (Cos (τ) + Cos (\frac{w_{2}}{w_{1}} τ)) {\dot{x}}_{1} \\ + E_{0} (Cos (τ) + Cos (\frac{w_{2}}{w_{1}} τ))\} d τ \\ = - \frac{7661471}{11520000} + \frac{1}{6400} t^{2} + \frac{1037}{1920} Cos (t) + \frac{2591}{19200} Cos (2 t) \\ - \frac{1}{28800} Cos (3 t) + \frac{1}{30720} Cos (4 t) + \frac{1}{120000} Cos (5 t) \\ ⋮ \end{matrix}

and the solution will be

(38)

\{\begin{matrix} x (t) = \lim_{i \to \infty} x_{i} (t), \\ y (t) = \lim_{i \to \infty} y_{i} (t) . \end{matrix}

Note that approximate solutions are calculated at $E_{0} = . 5$ .

Case III:

In this case the interaction of electromagnetic wave with two-color, orthogonal polarization and same amplitude is considered. Therefore,

(39)

\{\begin{matrix} \vec{E} = E_{0} Cos (w_{1} t) \hat{j} + E_{0} Cos (w_{2} t) \hat{k}, \\ \vec{B} = B_{0} Cos (w_{1} t) \hat{k} - B_{0} Cos (w_{2} t) \hat{j} . \end{matrix}

Substituting Eq. (39) in Eq. (1) yields:

(40)

\{\begin{matrix} m \ddot{x} = - e (v_{y} B_{0} Cos (w_{1} t) + v_{z} B_{0} Cos (w_{2} t)), \\ m \ddot{y} = - e (E_{0} Cos (w_{1} t) - v_{x} B_{0} Cos (w_{1} t)), \\ m \ddot{z} = - e (E_{0} Cos (w_{2} t) - v_{x} B_{0} Cos (w_{2} t)) . \end{matrix}

As the same as previous case and using

(41)

\{\begin{matrix} x = \frac{{xw}_{1}}{c}, \\ y = \frac{{yw}_{1}}{c}, \\ z = \frac{{zw}_{1}}{c}, \\ E = \frac{eE}{{mcw}_{1}}, \\ t = w_{1} t, \end{matrix}

we have following dimensionless equations:

(42)

\{\begin{matrix} \ddot{x} = - E_{0} Cos (t) \dot{y} - E_{0} Cos (\frac{w_{2}}{w_{1}} t) \dot{z}, \\ \ddot{y} = - E_{0} Cos (t) + E_{0} Cos (t) \dot{x}, \\ \ddot{z} = - E_{0} Cos (\frac{w_{2}}{w_{1}} t) + E_{0} Cos (\frac{w_{2}}{w_{1}} t) \dot{x} . \end{matrix}

To solve Eq. (42) by VIM, as the same as previous cases we have $λ_{1} (τ) = λ_{2} (τ) = λ_{3} (τ) = τ - t$ .

So, the variational iteration formula are

(43)

\begin{matrix} x_{n + 1} (t) = x_{n} (t) + \int_{0}^{t} (τ - t) {x_{n_{τ τ}} + E_{0} Cos (τ) {\dot{y}}_{n} + E_{0} Cos (\frac{w_{2}}{w_{1}} τ) {\dot{z}}_{n}} d τ, \\ y_{n + 1} (t) = y_{n} (t) + \int_{0}^{t} (τ - t) \{y_{n_{τ τ}} - E_{0} Cos (τ) {\dot{x}}_{n} + E_{0} Cos (τ)\} d τ, \\ z_{n + 1} (t) = z_{n} (t) + \int_{0}^{t} (τ - t) \{z_{n_{τ τ}} - E_{0} Cos (\frac{w_{2}}{w_{1}} τ) {\dot{x}}_{n} + E_{0} Cos (\frac{w_{2}}{w_{1}} τ)\} d τ, \end{matrix}

Using $x_{0} = - . 09 t, y_{0} = . 01 Cos (t)$ and $z_{0} = . 01 Cos (1.5 t)$ as initial approximations, other components of solutions can be obtained as follows

(44)

\begin{matrix} x_{1} (t) = x_{0} (t) + \int_{0}^{t} (τ - t) \{x_{0_{τ τ}} + E_{0} Cos (τ) {\dot{y}}_{0} + E_{0} Cos (\frac{w_{2}}{w_{1}} τ) {\dot{z}}_{0}\} d τ \\ = - \frac{7}{80} t - \frac{1}{1600} Sin (2 t) - \frac{1}{2400} Sin (3 t) - \frac{3}{490} Sin (\frac{7}{2} t), \\ x_{2} (t) = x_{1} (t) + \int_{0}^{t} (τ - t) \{x_{1_{τ τ}} + E_{0} Cos (τ) {\dot{y}}_{1} + E_{0} Cos (\frac{w_{2}}{w_{1}} τ) {\dot{z}}_{1}\} d τ \\ = \frac{121}{14400} t - \frac{109}{3200} Sin (2 t) - \frac{109}{10800} Sin (3 t), \\ ⋮ \end{matrix}

And

(45)

\begin{matrix} y_{1} (t) = y_{0} (t) + \int_{0}^{t} (τ - t) {y_{0_{τ τ}} - E_{0} Cos (τ) {\dot{x}}_{0} + E_{0} Cos (τ)} d τ \\ = - \frac{107}{200} + \frac{109}{200} Cos (t), \\ y_{2} (t) = y_{1} (t) + \int_{0}^{t} (τ - t) {y_{1_{τ τ}} - E_{0} Cos (τ) {\dot{x}}_{1} + E_{0} Cos (τ)} d τ \\ = - \frac{246157}{460800} + \frac{1741}{3200} Cos (t) + \frac{1}{12, 800} Cos (2 t) + \frac{1}{28800} Cos (3 t) \\ + \frac{1}{51200} Cos (4 t), \\ ⋮ \end{matrix}

(46)

\begin{matrix} z_{1} (t) = z_{0} (t) + \int_{0}^{t} (τ - t) \{z_{0_{τ τ}} - E_{0} Cos (\frac{w_{2}}{w_{1}} τ) {\dot{x}}_{0} + E_{0} Cos (\frac{w_{2}}{w_{1}} τ)\} d τ \\ = - \frac{209}{900} + \frac{109}{450} Cos (\frac{3}{2} t), \end{matrix}

(47)

\begin{matrix} z_{2} (t) = z_{1} (t) + \int_{0}^{t} (τ - t) \{z_{1_{τ τ}} - E_{0} Cos (\frac{w_{2}}{w_{1}} τ) {\dot{x}}_{1} + E_{0} Cos (\frac{w_{2}}{w_{1}} τ)\} d τ \\ = - \frac{23129}{99225} + \frac{8}{200} Cos (\frac{1}{2} t) + \frac{1741}{7200} Cos (\frac{3}{2} t) \end{matrix}

(48)

\begin{matrix} + \frac{1}{39200} Cos (\frac{7}{2} t) + \frac{1}{64800} Cos (\frac{9}{2} t), \\ ⋮ \end{matrix}

And the solution will be

(49)

\{\begin{matrix} x (t) = \lim_{i \to \infty} x_{i} (t), \\ y (t) = \lim_{i \to \infty} y_{i} (t), \\ z (t) = \lim_{i \to \infty} z_{i} (t) . \end{matrix}

Note that calculations are at $E_{0} = . 5$ and $\frac{w_{2}}{w_{1}} = 1.5$ .

5 Results and discussions

Studying Fig. 1a and b shows that the electron moves back and forth across the boundary twice during one cycle of the field, i.e. we have a normal motion of the electron surface at $2 w$ and generated harmonics oscillate with $w, 3 w, 5 w, \dots$ On the other hand, odd harmonics will be generated and these results are in excellent agreement with the experimental results (Brabec, 2008). In case II the incident electromagnetic wave is radiated with $w_{1} = w$ and $w_{2} = 2 w$ . As Fig. 2a and b shows dominant frequencies of electron along x-axis are $w, 2 w, and 3 w$ . Therefore, higher harmonics of odd and even order will be generated. The frequency of electrons $, w$ , along x-axis makes $w, 2 w, 3 w, \dots$ and $2 w, 3 w, 4 w, \dots$ frequencies. And the frequency of electrons, $2 w$ , along x-axis makes $w, 3 w, 5 w, \dots$ and $2 w, 4 w, 6 w, \dots$ frequencies. Also the frequency of electrons $, 3 w$ , along x-axis causes generated harmonics to have $w, 4 w, 7 w, \dots$ and $2 w, 5 w, 8 w, \dots$ . frequencies. It is clear that the gain of some frequencies such as $4 w, 5 wand 8 w$ is increased. The obtained results by VIM for case II, are the same as experimental results (Dohelstorm, 2007) and also indicate a very important physical result that is related to gain (Mirzanejad and Salehi, 2013). In the third case the incident electromagnetic wave is radiated with $w_{1} = w$ and $w_{2} = 1.5 w$ and orthogonal polarization. By studying Fig. 3a and b it is obvious that generated harmonics oscillate with $w, 2 w, 3 w, \dots$ and higher harmonics of even and odd order will be generated. In case III, obtained results by VIM are the same as experimental results (Zeng et al., 2007; Kim et al., 2005). Note that for solving mentioned equations by VIM there is no need to suppose any restrictions and we can solve them generally.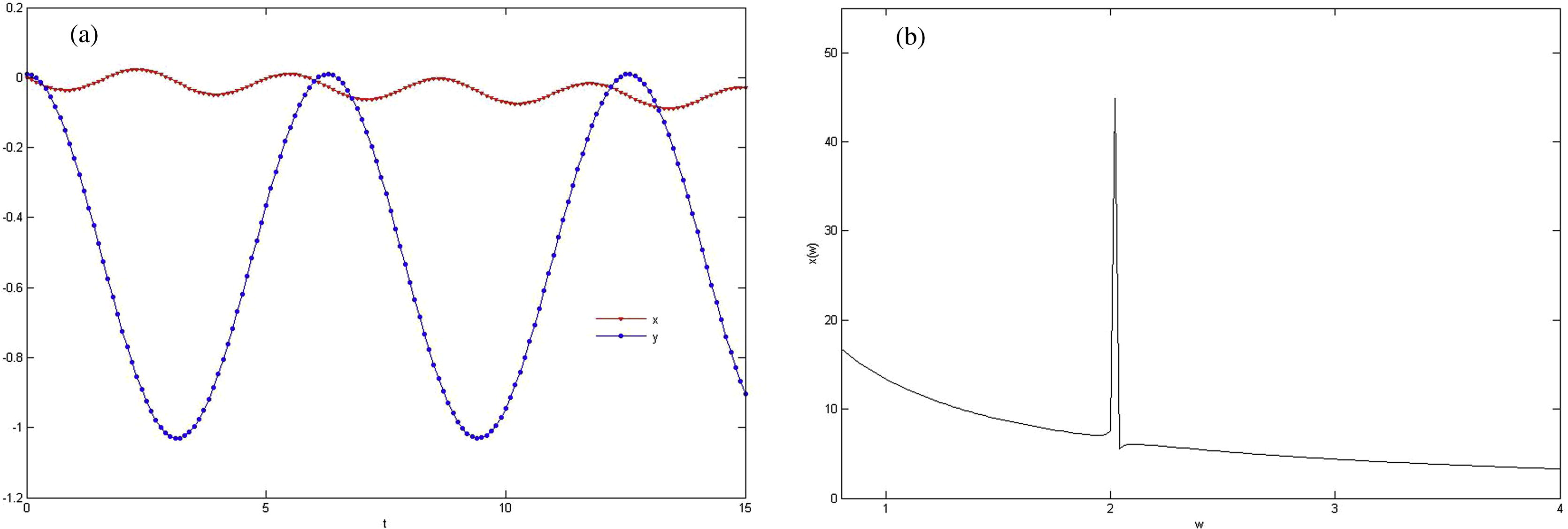

(a) Simulation of oscillation of electron along x-axis and y-axis. (b) Fourier transform of x ( t ) for the first case.

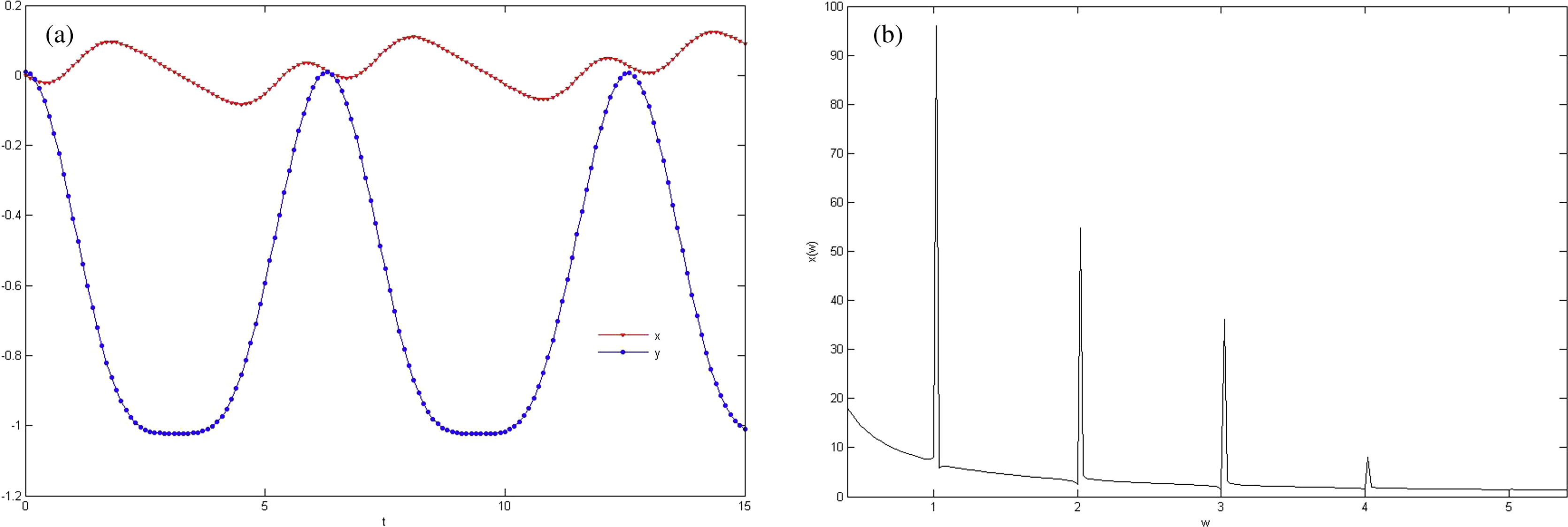
(a) Simulation of oscillation of electron along x-axis and y-axis. (b) Fourier transform of x ( t ) for the second case.

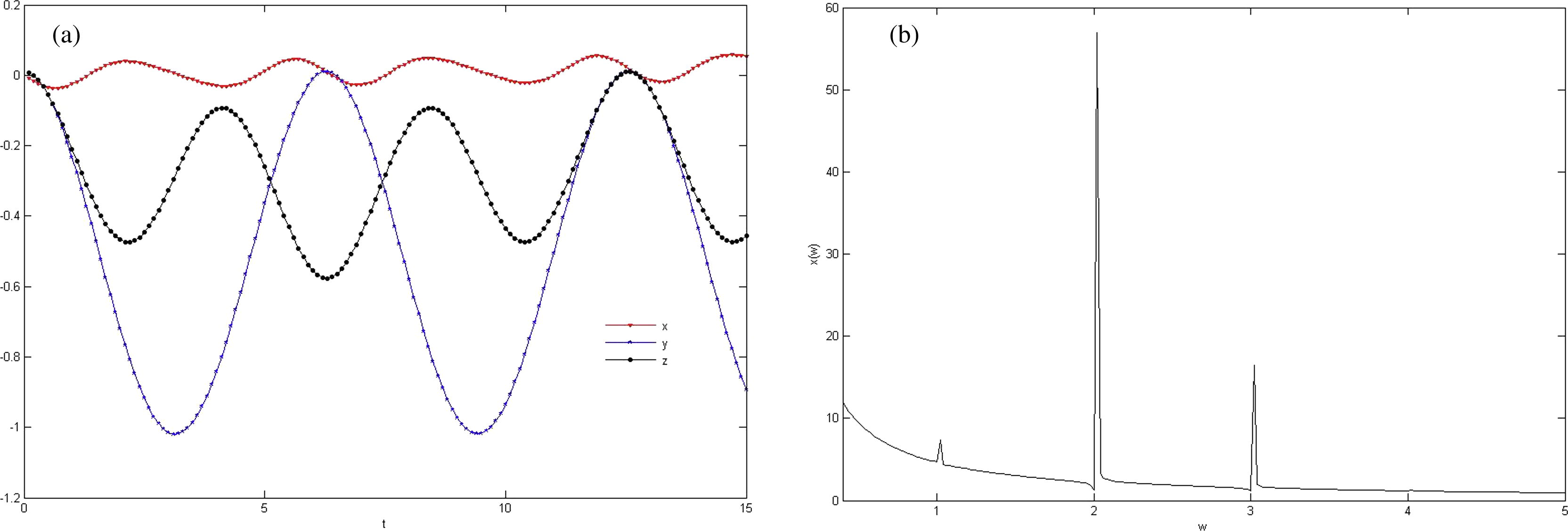
(a) Simulation of oscillation of electron along x-axis and y-axis. (b) Fourier transform of x ( t ) for the third case.

6 Conclusion

In this paper, we solved the equations that model the generation of Harmonics of higher order, using He’s Variational Iteration Method (VIM). Three cases were investigated and the obtained results indicate that by using this method a rapid convergent sequence is produced and this technique provides accurate approximations to the solution of related equations that are in excellent agreement with the experimental results. All calculations were done generally and we did not suppose any restriction that is necessary in experimental procedures and this approves that the applied technique is reliable and efficient to handle other equations and phenomena in physics. The computations associated with the cases in this paper were performed using Matlab.

References

Biazar J., Gholami M., Ebrahimi H., . Variational iteration method for linear and non linear systems of integro-differential equations. Int. Math. Forum.. 2010;5(64):3185-3191.
[Google Scholar]
Brabec T., . Strong Field Laser Physics. Springer Publication; 2008. pp. 300–310
Corkum P.B., . Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett.. 1993;71:1994-1997.
[Google Scholar]
Dorner R., Mergel V., Jagutzki O., Spielberger L., Ullrich J., Moshammer R., Schmidt-Bocking H., . Cold target Recoil Ion Momentum spectroscopy a momentum microscope to view atomic collision dynumics. Phys. Rep.. 2000;330:95-192.
[Google Scholar]
Dohelstorm, M., 2007. Strong field approximation for High order Harmonic Generation with $\frac{w}{2 w}$ laser fields. Lund. Report on Atomic, Physics, LRAP-381.
Ebadian E., Dastani N., . He’s homotopy perturbation method: An effective tool for solving a nonlinear syatem of two-dimensional Volterra–Fredholm integral equation. Math. Comput. Modelling.. 2012;55(3):1233-1244.
[Google Scholar]
Ganji Z.Z., Ganj D.D., Fereidoon A., Rostamiyan Y., . Efficency determination of radiators with temperature-dependent thermal conductivity using two He’s methods. Heat Transer Res.. 2009;40(14):333-349.
[Google Scholar]
Gharsseldien Z.M., Hemida K., . New technique to avoid noise terms on the solutions of inhomogeneous differential equations by using Adomian decomposition method. Commun. Nonlinear Sci. Numer. Simul.. 2009;14(3):685-696.
[Google Scholar]
Gholami M., Ghambari B., . Application of He’s variational iteration method for solution of the family of Kuramoto–Sivashinsky equations. J. King Saud Univ. Sci.. 2011;23(14):407-411.
[Google Scholar]
Hassan S.M., Alotaibi N.M., . Solitary wave solutions of the improved Kdv equation by VIM. Appl. Math. Comput.. 2010;217(6):2397-2403.
[Google Scholar]
Kim I.J., Kim C.M., Kim H.T., Lee G.H., Lee Y.S., Park J.Y., Jaeyun Cho D., Nam C.H., . Highly efficient high-harmonic generation in an orthogonally polarized two-color laser field. Phys. Rev. Lett.. 2005;94:243901.
[Google Scholar]
Kafash B., Delavarkhalafi A., Karbassi S.M., . Application of variational iteration method for Hamlton–Jacobi–Bellman equations. Appl. Math. Model.. 2013;37(6):3917-3928.
[Google Scholar]
Khader M.M., . Numerical and theoretical treatment for solving linear and non linear delay differential equations using variational iteration method. Arab. J. Math. Sci.. 2013;9(2):243-256.
[Google Scholar]
Matinfar M., Ghasemi M., . Variational homotopy perturbation method for the Zakharove–Kuznetsov equations. J. Math. Statist.. 2010;6(4):425-430.
[Google Scholar]
Matinfar M., Ghasemi M., . Application of Variational Iteration Method to nonlinear heat transfer equations using He’s Polynomials. Int. J. Numer. Methods Heat Fluid Flow. 2013;23(3):520-531.
[Google Scholar]
Moshammer R., Unverzagt M., Schmitt W., Ullrich J., Schmidt-Bocking H., . A 4 $π$ recoil-ion election momentum analysis: a high-resolution microscope for the investigation of the dynamics of atomic, molecular and nuclear reactions. Nucl. Instrum. Meth. B.. 1996;108:425-445.
[Google Scholar]
Mirzanejad S., Salehi M., . Two-color high harmonic generation: relativistic mirror effects and attosecond pulses. Phys. Rev. A.. 2013;87(6):063815.
[Google Scholar]
Rajeev M., Kushwaha S., . Homotopy perturbation method for a lmit case Stefan problem governed by fractional diffusion equation. Appl. Math. Model.. 2013;37(5):3589-3599.
[Google Scholar]
Sheikholeslami M., Ashorynejad H.R., Ganji D.D., Yildirim A., . Homotopy perturbation method for three-dimensional problem of condensation film on inclined rotating disk. Sci. Iran.. 2012;19(3):437-442.
[Google Scholar]
Sheikholeslami M., Ganji D.D., Ashorynejad H.R., Rokni H.B., . Analytical investigation of Jeffery–Hamel flow with high magnetic field and nano particle by Adomian decomposition method. Appl. Math. Mech. Engl. Ed.. 2012;33(1):1553-1564.
[Google Scholar]
Sheikholeslami M., Ganji D.D., Ashorynejad H.R., . Investigation of squeezing unsteady nanofluid flow using ADM. Powder Technol.. 2013;239:259-265.
[Google Scholar]
Ullrich J., Moshammer R., Dorn A., Dorner R., Schmidt L.H., Schmidt-Bocking H., . Recoil-ion and electron momentum spectroscopy. Rep. Progr. Phys.. 2003;66:1463.
[Google Scholar]
Voitiv A.B., Ullrich J., . On the inter-relation between ionization of light atoms by virtual and real photons. J. Phys. B. 2001;34:4513.
[Google Scholar]
Voitiv A.B., Najjari B., Moshammer R., Ullrich J., . Helium single ionization in relativistic collisions with highly charged ions. J. Phys. Rev. A. 2002;65:032707.
[Google Scholar]
Voitiv A.B., Najjari B., Ullrich J., . Double ionization of Helium by relativistic highly charged ion impact. JETP. 2005;127(3):583-586.
[Google Scholar]
Wazwaz A.M., Randolph R., Duan J., . Adomian decomposition method for solving the Volterra integral form of the Lane–Emden equations with the initial values and boundary conditions. Appl. Math. Comput.. 2013;219(10):5004-5019.
[Google Scholar]
Zeng z., Cheng y., Song x., Li R., Xu Z., . Generation of an extreme ultraviolet supercontinuum in a two-color laser field. Phys. Rev. Lett.. 2007;98:203901.
[Google Scholar]