Translate this page into:
Some applications of M-open sets in topological spaces
*Corresponding author. Tel.: +966 505345032 mhm977@hotmail.com (Mohammad Ayed Nighimish Al-Juhani)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Available online 11 November 2013
Peer review under responsibility of King Saud University.

Abstract
The aim of this paper is to introduce and investigate some new classes of mappings called contra-M-continuous mappings and almost contra-M-continuous mappings via M-open sets. Also, the relationships between these mappings and other types are discussed. Several properties of these new notions are investigated and the connections between them are studied.
Keywords
Contra-M-continuous
Almost contra-M-continuous mappings
M-connected and M-compact spaces
1 Introduction
In the recent literature, many topologists had focused their research in the direction of investigating different types of generalized continuity.
Dontchev (1996) introduced a new class of mappings called contra-continuity. Jafari and Noiri (2001, 2002) exhibited and studied among others a new weaker form of this class of mappings called contra-α-continuous and contra-precontinuous mappings. Also, a new weaker form of this class of mappings called contra-semicontinuous mappings was introduced and investigated by Dontchev and Noiri (1999). Contra-δ-precontinuous mapping was obtained by Ekici and Noiri (2006). A good number of researchers have also initiated different types of contra continuous like mappings in the papers (Caldas and Jafari, 2001; Ekici, 2004c, 2008a; Nasef, 2005; Al-Omari and Noorani, 2009; El-Magbrabi, 2010). The notion of M-open sets in topological spaces was introduced by El-Maghrabi and Al-Juhani (2011) and studied some of their properties. This paper is devoted to introduce and investigate a new class of mappings called contra-M-continuous mappings. Also, some of their fundamental properties are studied.
2 Preliminaries
Throughout this paper (X, τ) and (Y, σ) (simply, X and Y) represent topological spaces on which no separation axioms are assumed, unless otherwise mentioned. The closure of subset A of X, the interior of A and the complement of A is denoted by cl(A), int(A) and Ac or X/A respectively. A subset A of a space (X, τ) is called regular open (Stone, 1937) if A = int(cl(A)). A point x ∈ X is said to be a θ-interior point of A (Velicko, 1968) if there exists an open set U containing x such that U ⊆ cl(U) ⊆ A.
A point x ∊ X is called δ-cluster (Velicko, 1968) point of A if int(cl(V)) ∩ A ≠ ϕ, for every open set V of X containing x. The set of all θ-interior points of A is said to be the θ-interior set and a subset A of X is called θ-open if A = intθ(A). A subset A of a space (X, τ) is called preopen by Mashhour et al. (1982) or locally dense by Carson and Michael (1964) (resp. δ-preopen by Raychaudhuri and Mukherjee (1993), α-open by Njåstad (1965), β-open by Abd El-Monsef et al. (1983), semi-open by Levine (1963), a-open by Ekici (2008c), δ-semi-open by Park et al. (1997) θ-semi-open by Caldas et al. (2008), e-open by Ekici (2008b), e∗-open by Ekici (2009), b-open by Andrijevíc, (1996) or γ-open by El-Atik (1997), M-open by El-Maghrabi and Al-Juhani (2011) if A ⊆ int(cl(A)) (resp. A ⊆ int(clδ(A)), A ⊆ int(cl(int(A))), A ⊆ cl(int(cl(A))), A ⊆ cl(int(A)), A ⊆ int(cl(intδ(A))), A ⊆ cl(intδ(A)), A ⊆ cl(intθ(A)), A ⊆ cl(intδ(A)) ∪ int(clδ(A)), A ⊆ cl(int(clδ(A))), A ⊆ cl(int(A)) ∪ int(cl(A)) and A ⊆ cl(intθ(A)) ∪ int(clδ(A)). The complement of preopen (resp. δ-preopen, α-open, β-open, semi-open, a-open, γ-open, e-open, e∗-open, δ-semi-open, M-open, θ-semi-open) set is called preclosed (Mashhour et al., 1982) (resp. δ-preclosed (Raychaudhuri and Mukherjee, 1993), α-closed (Njåstad 1965), β-closed (Abd El-Monsef et al., 1983), semiclosed (Levine, 1963), α-closed (Ekici, 2008c), γ-closed (El-Atik, 1997), e-closed (Ekici, 2008b), e∗-closed (Ekici, 2009), δ-semiclosed (Park et al., 1997), M-closed (El-Maghrabi and Al-Juhani, 2011), θ-semiclosed (Caldas et al., 2008)). The family of all preopen (resp. δ-preopen, α-open, β-open, semi-open, γ-open, θ-semi-open, e-open, e∗-open, δ-semi-open, M-open) is denoted by PO(X) (resp. δ-PO(X), αO(X), βO(X), SO(X), γO(X), θ-SO(X), e-O(X), e∗O(X), δ-SO(X), MO(X)). The intersection of all M-closed (resp. θ-semi-closed, δ-preclosed, e-closed) sets containing A is called the M-closure by El-Maghrabi and Al-Juhani (2011) (resp. θ-semi-closure by Caldas et al. (2008), δ-preclosure by Raychaudhuri and Mukherjee (1993), e-closure by Ekici (2008b)) of A and it is denoted by M-cl(A) (resp. sclθ(A), pclδ(A), e-cl(A)). The union of all M-open (resp. θ-semi-open, δ-preopen, e-open) sets contained in A is called the M-interior (El-Maghrabi and Al-Juhani, 2011) (resp. θ-semi-interior (Caldas et al., 2008), δ-pre-interior (Raychaudhuri and Mukherjee, 1993), e-interior (Ekici, 2008b)) of A and it is denoted by M-int(A) (resp. sintθ(A), pintδ(A), e-int(A)).
The following definitions and results were introduced and studied.
A mapping f: (X, τ) → (Y, σ) is called contra-continuous (Dontchev, 1996) (resp. contra α-continuous (Jafari and Noiri, 2001), contra-θ-semicontinuous, contra semicontinuous (Dontchev and Noiri, 1999), contra precontinuous (Jafari and Noiri, 2002), contra-δ-precontinuous (Ekici and Noiri, 2006), contra-a-continuous (Ekici, 2008a), contra-e-continuous (Ekici, 2008a, Ghosh and Basu, 2012), contra-e∗-continuous(Ekici, 2008a), contra-b-continuous (Ekici, 2004e), contra β-continuous (Caldas and Jafari, 2001), contra-δ-semicontinuous (Ekici, 2004c)) if, f−1(V) is closed (resp. α-closed, θ-semiclosed, semiclosed, preclosed, δ-preclosed, a-closed, e-closed, e∗-closed, b-closed, β-closed, δ-semiclosed) in X for each open set in Y.
A mapping f: (X, τ) → (Y, σ) is called almost contra-θ-continuous (resp. almost contra-θ-semicontinuous, almost contra continuous, almost contra-super-continuous (Ekici, 2004f), almost contra δ-semicontinuous (Ekici, 2004d), almost contra-precontinuous (Ekici, 2004a), almost contra δ-precontinuous (Ekici, 2004b), almost contra-α-continuous (Baker, 2011), almost contra-a-continuous (Ekici, 2007) almost contra-e-continuous (Ekici, 2007), almost contra-e∗-continuous (Ekici, 2007), almost contra-γ-continuous (Ekici, 2005), almost contra-β-continuous, almost contra semicontinuous) if, f−1(V) is θ-closed (resp. θ-semiclosed, closed, δ-closed, δ-semiclosed, preclosed, δ-preclosed, α-closed, a-closed, e-closed, e∗-closed, γ-closed, β-closed, semiclosed) in X for each regular open set of Y.
Let A be a subset of space (X, τ). Then:
(i) the kernel of A (Mrsevic, 1986) is given by ker(A) = ∩{U∈τ: A ⊆ U},
(ii) the M-boundary of A (El-Maghrabi and Al-Juhani, 2011) is given by M-b(A) = M-cl(A)/M-int(A)
Lemma 2.1 Jafari and Noiri (1999)
The following properties are holds for two subsets A, B of a topological space (X, τ):
(i) x ∈ ker(A) if and only if A ∩ F ≠ ϕ, for any closed set F of X containing x,
(ii) A ⊆ ker(A) and A = ker(A), if A is open in X,
(iii) If A ⊆ B, then ker(A) ⊆ ker(B).
A topological space (X, τ) is said to be:
(i) Urysohn (Singal and Mathur, 1969) if, for each two distinct points x, y of X, there exist two open sets U and V such that x ∈ U, y ∈ V and cl(U) ∩ cl(V) = ϕ,
(ii) ultra Hausdorff (Staum, 1974) if, for each two distinct points x, y of X, there exist two closed sets U and V such that x ∈ U, y ∈ V and U ∩ V = ϕ,
(iii) ultra normal (Staum, 1974) if for each pair of non-empty disjoint closed sets can be separated by disjoint clopen sets.
(iv) weakly Hausdorff (Soundararajan, 1971) if each element of X is the intersection of regular closed sets of X,
(v) strongly S-closed (Joseph and Kwack, 1980) (resp. S-closed (Dontchev, 1996), S-Lindelöff (Ekici, 2004a), countably S-closed (Dlaska et al., 1994) if for closed (resp. regular closed, regular closed, countably regular closed) cover of X has a finite (resp. finite, countable, finite) subcover.
3 Contra-M-continuous mappings
A mapping f: (X, τ) → (Y, σ) is called contra-M-continuous, if f−1(U) ∈ MC(X), for every open set U of Y.
According to Definitions 2.1, 3.1, the implications between these types of functions are given by the following diagram.
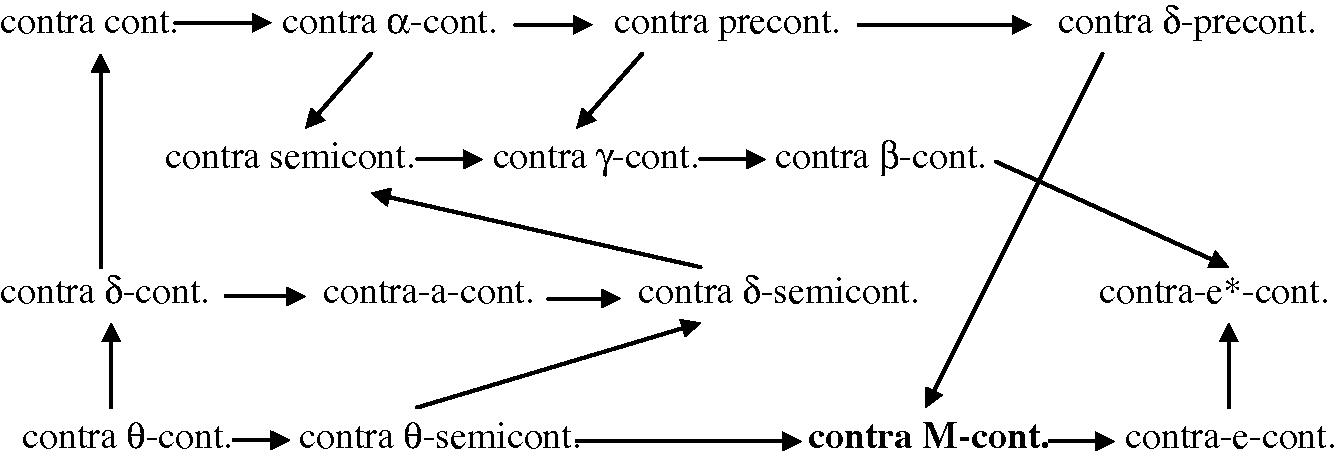
The converses of these implications need not be true in general and by the following examples and by Ekici (2008a,b,c,d,e); Ekici and Noiri (2006)).
Let X = {a, b, c, d} with τ = {X, ϕ, {a}, {b}, {a, b}, {a, b, c}, {a, b, d}} and Y = {a, b, c} with σ = {Y, ϕ, {a}, {b}, {a, b}}. Hence a mapping f: (X, τ) → (Y, σ) which defined by f(a) = f(c) = c, f(b) = a and f(d) = b is contra-e-continuous but not contra-M-continuous. Since, f−1({a, b}) = {b, d} is not M-closed of X.
Let X = Y = {a, b, c} with τ = {X, ϕ, {a}, {b}, {a, b}} and σ = {Y, ϕ, {a}, {b, c}}. If, f: (X, τ) → (Y, σ) which defined by the identity mapping, then f is contra-M-continuous mapping but not contra δ-precontinuous. Since, f−1({a}) = {a} is not δ-preclosed set of X. Also, f is contra-M-continuous mapping but not contra θ-semicontinuous. Since, f−1({b, c}) = {b, c} is not θ-semiclosed set of X.
For a mapping f: (X, τ) → (Y, σ), the following statements are equivalent:
(i) f is contra-M-continuous,
(ii) for each x ∈ X and each closed subset F of Y containing f(x), there exist U ∈ MO(X) such that x ∈ U and f(U) ⊆ F,
(iii) for every closed subset F of Y, f−1(F) ∈ MO(X),
(iv) f(M-cl(A)) ⊆ ker(f(A)), for each A ⊆ X,
(v) M-cl(f−1(B)) ⊆ f−1(ker(B)), for each B ⊆ Y.
(i)→(ii). Let x ∈ X and F be any closed set of Y containing f(x). Then x ∈ f−1(F). Hence by hypothesis, we have f−1(Y/F) is M-closed in X and hence f−1(F) is M-open set of X containing x. We put U = f−1(F), then x ∈ U and f(U) ⊆ F.
(ii)→(iii). Let F be any closed set of Y and x ∈ f−1(F). Then f(x) ∈ F. Hence by hypothesis, there exists an M-open subset U containing x such that f(U) ⊆ F, this implies that, x ∈ U ⊆ f−1(F). Therefore, f−1(F) = ∪{U: x ∈ f−1(F)} which is M-open in X. Then f is contra-M-continuous.
(iii)→(iv). Let A be any subset of X and y ker(f(A)). Then by Lemma 2.1, there exists a closed set F of Y containing y such that f(A) ∩ F = ϕ. Hence, A ∩ f−1(F) = ϕ and M-cl(A) ∩ f−1(F) = ϕ. Then f(M-cl(A)) ∩ F = ϕ and y f(M-cl(A)). Therefore, f(M-cl(A)) ⊆ ker(f(A)).
(iv)→(v). Let B be any subset of Y. Then by hypothesis and Lemma 2.1, we have f(M-cl(f−1(B))) ⊆ ker(f(f−1(B))) ⊆ ker(B). Thus M-cl(f−1(B)) ⊆ f−1(ker(B)).
(v)→(i). Let V be any open subset of Y. Then by hypothesis and Lemma 2.1, M-cl(f−1(V)) ⊆ f−1(ker(V)) = f−1(V). Therefore, f−1(V) is M-closed in X. Hence, f is contra-M-continuous.
Definition 3.2 El-Maghrabi and Al-Juhani (2013a,b)
A mapping f: (X, τ) → (Y, σ) is called:
(i) M-continuous if, f−1(U) ∈ MO(X), for each U ∈ σ,
(ii) M-irresolute if, f−1(U) ∈ MO(X), for each U ∈ MO(Y),
(iii) pre-M-open if, f(U) ∈ MO(Y), for each U ∈ MO(X),
(iv) pre-M-closed if, f(U) ∈ MC(Y), for each U ∈ MC(X).
If a mapping f: (X, τ) → (Y, σ) is contra-M-continuous and Y is regular, then f is M-continuous.
Let x ∈ X and V be an open set of Y containing f(x). Since Y is a regular space, then there exists an open set G of Y such that f(x) ⊆ G ⊆ cl(G) ⊆ V. But, if f is contra-M-continuous, then there exists U ∈ MO(X) such that x ∈ U and f(U) ⊆ cl(G) ⊆ V. Hence, f is M-continuous. □
The composition of two contra-M-continuous mappings need not be contra-M-continuous as shown by the following example.
Let X = Y = Z = {a, b, c, d}, with topologies τx = {X, ϕ,{a},{b}, {a, b}}, τy is an indiscrete topology and τz = {Z, ϕ, {a, d}}. Then the identity mappings f: (X, τx) → (Y, τy) and g: (Y, τy) → (Z, τz) are contra-M-continuous mappings, but g o f is not contra-M-continuous. Since, f−1({a, d}) is not M-closed of X.The next theorems give the conditions under which the composition of two contra-M-continuous mappings is also contra-M-continuous.
For two mappings f: (X, τx) → (Y, τy) and g: (Y, τy) → (Z, τz), the following properties are hold:
(i) If f is contra-M-continuous and g is continuous mappings, then g o f is contra-M-continuous,
(ii) If f is M-irresolute and g is contra-M-continuous mappings, then g o f is contra-M-continuous.
(i) Let U ∈ τz and g be a continuous mapping. Then g−1(U) ∈ τy. But, f is contra-M-continuous, then (g o f)−1(U) ∈ MC(X). Hence, g o f is contra-M-continuous.
(ii) Let U ∈ τz and g be a contra-M-continuous mapping. Then g−1(U) ∈ MC(Y). But, f is M-irresolute, then (g o f)−1(U) ∈ MC(X). Hence, g o f is contra-M-continuous. □
Let f: X → Y be a surjective M-irresolute and pre-M-open mapping. Then g o f: X → Z is contra-M-continuous if and only if g is contra-M-continuous.
Necessity. Obvious from Theorem 3.3.Sufficiency. Let g o f: X → Z be a contra-M-continuous mapping and F be a closed set of Z. Then (g o f)−1(F) ∈ MO(X). Since f is surjective pre-M-open, then g−1(F) ∈ MO(Y). Therefore, g is contra-M-continuous. □
Definition 3.3 El-Maghrabi and Al-Juhani, 2013c
A topological space (X, τ) is called:
(i) M-connected if X cannot be expressed as the union of two disjoint non-empty M-open sets of X,
(ii) M-normal if, for every pair of disjoint closed sets F1 and F2, there exist disjoint M-open sets U and V such that F1 ⊆ U and F2 ⊆ V,
(iii) M-T1-space if for every two distinct points x, y of X, there exist two M-open sets U, V such that x ∈ U, y U and x V, y ∈ V.
(iv) M-T2-space or M-Hausdorff space if for every two distinct points x, y of X, there exist two disjoint M-open sets U, V such that x ∈ U and y ∈ V.
If, f: (X, τ) → (Y, σ) is an injective closed and contra-M-continuous mappings, and Y is ultra normal, then X is M-normal.
Let F1 and F2 be two disjoint closed subsets of X. Since f is closed injection, then f(F1) and f(F2) are two disjoint closed subsets of Y and since Y is ultra normal space, then there exist two disjoint clopen sets U and V such that f(F1) ⊆ U and f(F2) ⊆ V. Hence, F1 ⊆ f−1(U) and F2 ⊆ f−1(V). Since f is injective contra-M-continuous, then f−1(U) and f−1(V) are two disjoint M-open sets of X. Therefore, X is M-normal. □
If, f: (X, τ) → (Y, σ) is a contra-M-continuous mapping and X is M-connected, then Y is not a discrete space.
Suppose that Y is a discrete space and U any subset of Y. Then U is open and closed set in Y. Since f is contra-M-continuous, f−1(U) is M-closed and M-open in X which is a contradiction with the fact that X is M-connected. Hence, Y is not discrete space. □
If, f: (X, τ) → (Y, σ) is an injective contra-M-continuous mapping and Y is an Urysohn space, then X is M-T2.
Let x, y ∈ X and x ≠ y. By hypothesis, f(x) ≠ f(y). Since Y is an Urysohn space, there exist two open sets U and V of Y such that f(x) ∈ U, f(y) ∈ V and cl(U) ∩ cl(V) = ϕ. Since f is contra-M-continuous, then there exist two M-open sets P and Q such that x ∈ P, y ∈ Q and f(P) ⊆ cl(U), f(Q) ⊆ cl(V). Then f(P) ∩ f(Q) = ϕ and hence, P ∩ Q = ϕ. Therefore, X is M-T2. □
If f: (X, τ) → (Y, σ) is an injective contra-M-continuous mapping and Y is an ultra Hausdorff space, then X is M-T2.
A mapping f: (X, τ) → (Y, σ) is called weakly-M-continuous if, for each x ∈ X and each open set V of Y containing f(x), there exists U ∈ MO(X) such that x ∈ U and f(U) ⊆ cl(V).
If f: (X, τ) → (Y, σ) is a contra-M-continuous mapping, then f is weakly-M-continuous.
Let x ∈ X and V ∈ σ containing f(x). Then cl(V) is closed set in Y. Since f is contra-M-continuous, then f−1(cl(V)) ∈ MO(X) and containing x. If we put U = f−1(cl(V)), then f(U) ⊆ cl(V). Hence, f is weakly-M-continuous. □
The converse of Theorem 3.8 is not true as shown by the following example.
Let X = {a, b, c, d} and Y = {a, b, c} with topologies τ = {X, ϕ, {a}, {b}, {a, b}, {a, b, c}, {a, b, d}}and σ = {Y, ϕ, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}}. Then a mapping f: (X, τ) → (Y, σ) which defined by f(a) = f(c) = c, f(b) = a and f(d) = b is weakly-M-continuous mapping but, it is not contra-M-continuous. Since, f−1({a, b}) = {b, d} is not M-closed of X.
4 Almost contra-M-continuous mappings
Now, we introduce a new type of continuity called almost contra-M-continuity which is weaker than almost contra-δ-precontinuity (Ekici, 2004b), almost contra-θ-semicontinuity and stronger than almost contra-e-continuity (Ekici, 2007).
A mapping f: (X, τ) → (Y, σ) is called almost-M-continuous if, for each x ∈ X and each open set V of Y containing f(x), there exists U ∈ MO(X) such that x ∈ U and f(U) ⊆ int(cl(V)), equivalently, f−1(V) is M-open in X for every regular open set V of Y.
A mapping f: (X, τ) → (Y, σ) is called almost-M-continuous if and only if for each x ∈ X and each regular open set V of Y containing f(x), there exists U ∈ MO(X) containing x such that f(U) ⊆ V.
Necessity. Let V ⊆ Y be regular open set containing f(x). Then x ∈ f−1(V). But f is almost-M-continuous, then f−1(V) = U is regular open set of X containing x such that f(U) = f f−1(V) ⊆ V. □
Sufficiency. Let V⊆ Y be regular open set. We need to prove that f−1(V) ∈ MO(X). Suppose that x ∈ f−1(V). Then f(x) ∈ V. By hypothesis, there exists U ∈ MO(X) containing x such that f(U) ⊆ V. Hence x ∈ U ⊆ f−1(f(U)) ⊆ f−1(V). Then f−1(V) = ∪ {U: x ∈ U} is an M-open set of X. Therefore, f is almost-M-continuous.
A mapping f: (X, τ) → (Y, σ) is called almost contra-M-continuous if, f−1(V) is M-closed in X, for every regular open set V of Y.
The implication between some types of mappings of Definitions 2.2, 4.2, is given by the following diagram.
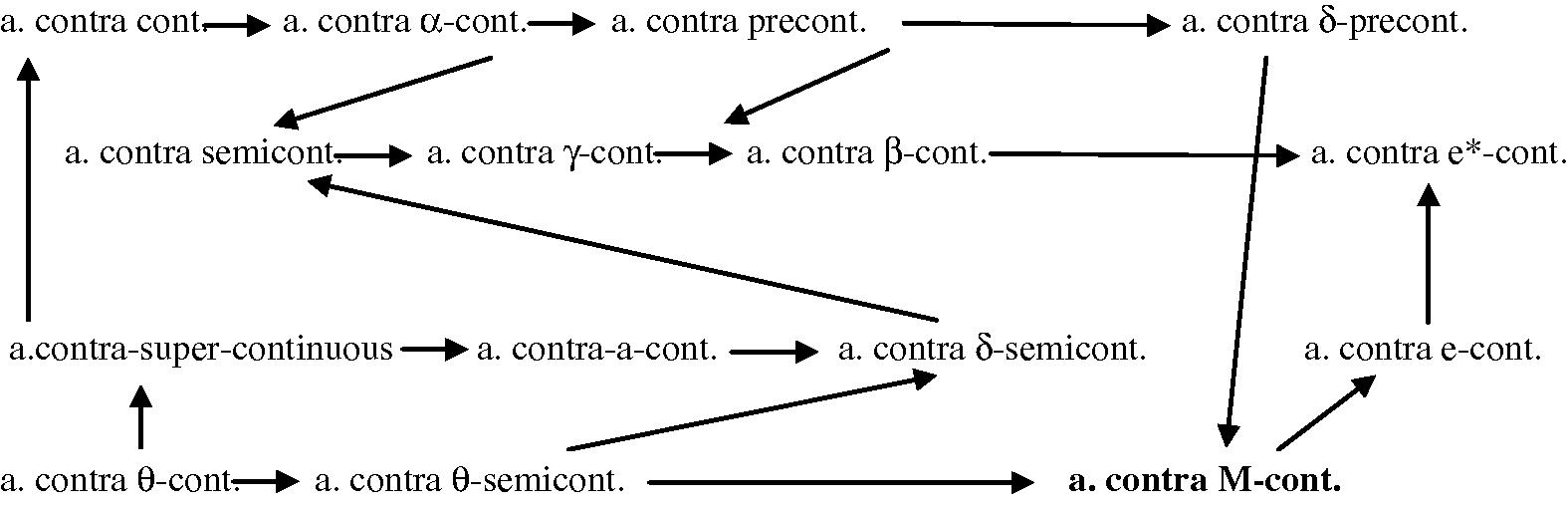
The converse of these implications need not be true in general and by the following examples and by Ekici (2007, 2004a,b,c, 2005)
Let X = Y = {a, b, c} with topologies τ = {X, ϕ, {a}, {b}, {a, b}}andσ = {Y, ϕ, {a}, {b}, {a, b}, {b, c}}. If f: (X, τ) → (Y, σ) is the identity mapping, then f is almost contra-M-continuous mapping but not almost contra δ-precontinuous. Since,f−1({a}) = {a} is not δ-preclosed in X.
Let X = Y = {a, b, c, d} with topologies τ = {X, ϕ, {a},{c},{a, b}, {a, c}, {a, b, c}, {a, c, d}} and σ = {Y, ϕ, {a}, {b}, {a, b},{a, b, c}, {a, b, d}}.If f: (X, τ) → (Y, σ) is the identity mapping, then f is almost contra-M-continuous mapping but not almost contra-θ-semicontinuous. Since, f−1({a}) = {a} is not θ-semiclosed in X.
Let X = Y = {a, b, c, d} with topologies τ = {X, ϕ, {a},{b},{a, b}, {a, b, c}, {a, b, d}} and σ = {Y, ϕ, {a, b, c}, {b, c}, {a, d}, {a}}. If f: (X, τ) → (Y, σ) is the identity mapping, then f is almost contra-e-continuous mapping but not almost contra M-continuous. Since, f−1({b, c}) = {b, c} is not M-closed in X.
For a mapping f: (X, τ) → (Y, σ), the following statements are equivalent:
(i) f is almost contra-M-continuous,
(ii) f−1(F) is M-open in X, for every regular closed set F of Y, for each x ∈ X and each regular closed set F of Y containing f(x), there exists U ∈ MO(X) such that x ∈ U and f(U) ⊆ F,
(iii) for each x ∈ X and each regular open set V of Y not containing f(x), there exists an M-closed set K of X not containing x such that f−1(V) ⊆ K.
Proof i
(i)→(ii). Let F be any regular closed set of Y. Then Y/F is regular open. By hypothesis, f−1(Y/F) = X/f−1(F) ∈ MC(X). Therefore, f−1(F) ∈ MO(X). □
(ii)→(i). Obvious.
(ii)→(iii). Let F be any regular closed set of Y containing f(x). Then by hypothesis, f−1(F) ∈ MO(X) and x ∈ f−1(F). Put U = f−1(F), then f(U) ⊆ F.
(iii)→(ii). Let F be any regular closed set of Y and x ∈ f−1(F). By hypothesis, there exist U ∈ MO(X) such that x ∈ U and f(U) ⊆ F. Hence, x ∈ U ⊆ f−1(F). That implies f−1(F) = ∪{U: x ∈ f−1(F)} Therefore, f−1(F) ∈ MO(X).
(iii)→(iv). Let V be any regular open set of Y non-containing f(x). Then Y/V is regular closed set of Y containing f(x). By (iii), there exists U ∈ MO(X) such that x ∈ U and f(U) ⊆ Y/V. Then U ⊆ f−1(Y/V) ⊆ X/f−1(V) and so f−1(V) ⊆ X/U. Since U ∈ MO(X), then X/U = K is M-closed set of X not containing x and f−1(V) ⊆ K.
(iv)→(iii). Obvious. □
The composition of two almost contra-M-continuous mappings need not be almost contra-M-continuous as shown by the following example.
Let X = Y = Z = {a, b, c, d}, with topologies τx = {X, ϕ,{a},{b}, {a, b}, {a, b, c}, {a, b, d}}, τy is an indiscrete topology and τz = {Z, ϕ, {a}, {b}, {a, b}, {a, d}, {a, b, c}, {a, b, d}}. Then the identity mappings f: (X, τx) → (Y, τy) and g: (Y, τy) → (Z, τz) are almost contra-M-continuous mappings, but g o f is not almost contra-M-continuous. Since, f−1({a, d}) = {a, d} is not M-closed of X.
For two mappings f: (X, τx) → (Y, τy) and g: (Y, τy) → (Z, τz), the following properties are hold:
(i) If, f is a surjective pre-M-open and g o f: X → Z is almost contra-M-continuous, then g is almost contra-M-continuous.
(ii) If, f is a surjective pre-M-closed and g o f: X → Z is almost contra-M-continuous, then g is almost contra-M-continuous.
Let V ⊆ Z be regular closed set. Since, g o f is almost contra-M-continuous, then (g o f)−1(V) ∈ MO(X). But, f is surjective pre-M-open, then g−1(V) ∈ MO(Y). Therefore, g is almost contra-M-continuous. □(i) Obvious. □
If f: (X, τ) → (Y, σ) is an injective almost contra-M-continuous mapping and Y is weakly Hausdorff, then X is M-T1.
Let x, y be two distinct points of X. Since f is injective, then f(x) ≠ f(y) and since Y is weakly Hausdorff, there exist two regular closed sets U and V such that f(x) ∈ U, f(y) U and f(x) V, f(y) ∈ V. Since f is an almost contra-M-continuous, we have f−1(U) and f−1(V) are M-open sets in X such that x ∈ f−1(U), y f−1(U) and x f−1(V), y ∈ f−1(V) and f−1(U) ∩ f−1(V) = ϕ. Hence X is M-T1. □
A topological space (X, τ) is said to be:
(i) M-compact if every M-open cover of X has finite subcover,
(ii) countably M-compact if every countable cover of X by M-open sets has a finite subcover,
(iii) M-Lindelöff if every M-open cover of X has a countable subcover.
If f: (X, τ) → (Y, σ) is a surjective almost contra-M-continuous mapping, then the following statements are hold:
(i) If X is M-compact, then Y is S-closed,
(ii) If X is countably M-compact, then Y is countably S-closed,
(iii) If X is M-Lindelöff, then Y is S-Lindelöff.
Let {Vi: i ∈ I} be any regular closed cover of Y and f be almost contra-M-continuous. Then {f−1(Vi): ∈ I}is M-open cover of X. But X is M-compact, there exists a finite subset Io of I such that X = ∪{f−1(Vi): i ∈ Io}, hence Y = ∪ {f f−1(Vi): i ∈ Io} and then Y = ∪{Vi: i∈Io}. Hence Y is S-closed.
(i) Similar to (i).
(ii) Similar to (i). □
5 Conclusion
The authors study contra-M-continuous and almost contra-M-continuous mappings. Continuity is a valuable subject in many branches of maths. Properties and characterizations of contra-M-continuous and almost contra-M-continuous mappings are investigated. Also, the relationships between this paper and many recent papers are introduced. The relationships between this paper and the related good papers in the literature are good and important.
Acknowledgments
We would like to express our sincere gratitude to the referees for their valuable suggestions and comments which improved the paper.
References
- β-Open sets and β-continuous mappings. Bull. Fac. Sci. Assiut Univ.. 1983;12(1):77-90.
- [Google Scholar]
- Some properties of contra-b-continuous and almost contra-b-continuous functions. European J. Pure. Appl. Math.. 2009;2(2):213-220.
- [Google Scholar]
- Weakly contra almost -continuous functions. Int. J. contemp. Math. Sci.. 2011;6(13):601-610.
- [Google Scholar]
- Some properties of contra-β-continuous functions. Mem. Fac. Sci. Kochi. Univ.. 2001;22:19-28.
- [Google Scholar]
- On θ -semi-open sets and separation axioms in topological spaces, Carpathian. J. Math.. 2008;24(1):13-22.
- [Google Scholar]
- Contra-continuous functions and strongly S-closed spaces. Int. J. Math. Math. Sci.. 1996;19:303-310.
- [Google Scholar]
- Almost contra-precontinuous functions. Bull. Malaysian Math. Sci. Soc.. 2004;27(1):53-65.
- [Google Scholar]
- (δ-pre, s)-Continuous functions. Bull. Malaysian Math. Sci. Soc.. 2004;27(2):237-251.
- [Google Scholar]
- On a weaker form of RC-continuity. Analele Univ. Vest din Timisoara Seria Matematica – Informatica, XLII, fasc.. 2004;1:79-91.
- [Google Scholar]
- Ekici, E., 2004f. Almost contra-super-continuous function, Studii si Cercet̆ari Stiin¸tifice, Seria: Matematic̆a, Universitatea din Bac̆au, 14, 31- 42.
- Ekici, E., 2005. On the notion of (ÃŽÂ3, s)-continuous functions, Demonstratio Mathematica,Vol. XXXVIII No 3, 715-727.
- On e-open sets, DP∗-sets and DPE∗-sets and decompositions of continuity. Arabian J. Sci. and Eng.. 2008;33(2A):269-282.
- [Google Scholar]
- On a-open sets, A∗-sets and decompositions of continuity and super- continuity. Annales Univ. Sci. Budapest.. 2008;51:39-51.
- [Google Scholar]
- El-Atik, A.A., 1997. A study on some types of mappings on topological spaces, M. Sci. Thesis Tanta Univ, Egypt.
- Some properties of contra–continuous mappings. Int. J. General Topol.. 2010;3(1–2):55-64.
- [Google Scholar]
- El-Maghrabi, A.I., Al-Juhani, M.A., 2013. Further properties on M-continuity, Proc. Math. Soc. Egypt.
- Contra–continuous functions between topological spaces. Iranian. Int. J. Sci.. 2001;2:153-167.
- [Google Scholar]
- On contra-precontinuous functions. Bull. Malaysian Math. Sc. Soc.. 2002;25:115-128.
- [Google Scholar]
- Semi-open sets and semicontinuity in topological spaces. Amer. Math. Monthly. 1963;70:36-41.
- [Google Scholar]
- On precontinuous and weak precontinuous mappings. Proc. Math. Phys. Soc. Egypt. 1982;53:47-53.
- [Google Scholar]
- On pairwise R and pairwise R1 bitopological spaces. Bull. Math. Soc. Sci. Math. R. S. Roumanie. 1986;30:141-148.
- [Google Scholar]
- Some properties of contra–continuous functions. Chaos Solitons Fractals. 2005;24:471-477.
- [Google Scholar]
- On δ-semi-open sets in topological spaces. J. Indian Acad. Math.. 1997;19(1):59-67.
- [Google Scholar]
- On δ-almost continuity and δ-preopen sets. Bull. Inst. Math. Acad. Sinica.. 1993;21:357-366.
- [Google Scholar]
- Weakly Hausdorff spaces and the cardinality of topological spaces in general topology and its relations to modern analysis and algebra III. Proc. Conf. Kanpur (1968), Acad. Prague. 1971;2:301-306.
- [Google Scholar]
- The algebra of bounded continuous functions into a non-archimedean field. Pacific J. Math.. 1974;50:169-185.
- [Google Scholar]
- Application of the theory of Boolean rings to general topology. Tams.. 1937;41:375-381.
- [Google Scholar]







