Challenge in the variational iteration method – A new approach to identification of the Lagrange multipliers

1 Introduction

From the Lagrange multiplier method (Inokuti et al., 1978), the variational iteration method (VIM), which was first proposed by (He, 1998, 1999) and systematically elucidated in (He and Wu, 2007), has been worked out over a number of years by numerous authors. Since there is no need to handle nonlinear terms in an equation and it results in approximate solutions with high accuracies, the analytical method caught much attention in the past ten years, and it has matured into a relatively fledged theory thanks to the efforts of many researchers, notably (Abbasbandy, 2007; Noor and Mohyud-Din, 2008; Xu, 2009; Geng, 2010; Jafari and Khalique, 2012) to mention only a few. For a relatively comprehensive survey on the concepts, theory and applications of the method, readers are referred to review articles (He and Wu, 2007; He, 2012).

Recently, Laplace transform is adopted in some famous analytical methods (e.g., the Laplace Adomian decomposition method (LAPM) (Tsai and Chen, 2010; Zeng and Qin, 2012) and the homotopy perturbation method (Javidi and Raji, 2012)) to simplify the solution process and improve solution's accuracy. However, their applications mainly limit to the applications in differential equations with constant coefficients. Though the VIM can deal with such problems, the identification of the Lagrange multiplier is complex if not impossible. To solve the problem, the VIM is reconstructed and Laplace transform is adopted in simple and accurate identification of the multipliers.

2 A novel modification of the variational iteration method

We use the following general nonlinear equation to illustrate its basic idea of the VIM:

The basic character of the method is to construct the following correction functional for Eq. (1)

The Lagrange multiplier can be identified as (He and Wu, 2007)

Now considering the system (1) with variable coefficients and assuming the linear term as

1. Take the Laplace transform on (1), then the iteration formula becomes

   (5)
   $$U_{n+1}(s)=U_n(s)+\lambda \left[s^m{U}_n(s)-{\displaystyle \sum _{i=0}^{m-1}}{u}^{(i)}(0)s^{m-i-1}+L\left({\displaystyle \sum _{i=0}^{m-1}}{a}_i{u}_n^{(i)}\right)+L\left({\displaystyle \sum _{i=0}^{m-1}}{b}_i(t)u_n^{(i)}\right)+L(N[u_n]-g(t))\right]$$ where U(s) is Laplace transform of u(t) and s is a complex variable.

2. Consider the terms $L\left({\sum }_{i=0}^{m-1}{b}_i(t)u^{(i)}\right)$ and L(N[u_n]) as restricted variations. Make Eq. (5) stationary with respect to U_n

   (6)
   $$\delta U_{n+1}(s)=\delta U_n(s)+\lambda \left[s^m\delta U_n(s)+{\displaystyle \sum _{i=0}^{m-1}}{a}_i{s}^i\delta U_n(s)\right]\text{.}$$ From Eq. (6), we can determine the Lagrange multiplier as follows $$\lambda (s)=-\frac{1}{{\displaystyle \sum _{i=0}^m}{a}_i{s}^i}\text{,}{a}_m=1\text{.}$$

3. The variational iteration formula is obtained through the inverse Laplace transform L⁻¹: $$u_{n+1}(t)=u_n(t)+L^{-1}\left[\lambda (s)\left[s^m{U}_n(s)-{\displaystyle \sum _{k=0}^{m-1}}{u}^{(k)}(0)s^{m-k-1}+L\left({\displaystyle \sum _{i=0}^{m-1}}{a}_i{u}_n^{(i)}\right)+L\left({\displaystyle \sum _{i=0}^{m-1}}{b}_i(t)u_n^{(i)}\right)+L\left(N[u_n]-g(t)\right)\right]\right]=u_0+L^{-1}\left[\lambda (s)L({\displaystyle \sum _{i=0}^{m-1}}{b}_i(t)u_n^{(i)}+N[u_n])\right]\text{,}$$ where the initial iteration value can be determined as $$u_0=L^{-1}\left[\lambda (s)\left[-{\displaystyle \sum _{k=0}^{m-1}}{u}^{(k)}(0)s^{m-k-1}-\left({\displaystyle \sum _{i=0}^{m-1}}{a}_i{\displaystyle \sum _{k=0}^{i-1}}{u}^{(k)}(0)s^{i-1-k}\right)-L\left[g(t)\right]\right]\right]\text{.}$$

4. Let $u_n={\sum }_{j=0}^n{v}_j$ and apply the Adomian decomposition method (ADM) (Adomian, 1994) to expand the term N[u] as ${\sum }_{j=0}^{\infty }{A}_j\text{.}$ Then the iteration formula reads $$\left\{\begin{array}{c}{v}_{j+1}=L^{-1}\left[\lambda (s)L({\displaystyle \sum _{i=0}^{m-1}}{b}_i(t)v_j^{(i)}+A_j)\right]\text{,}\hfill \\ v_0=u_0\text{,}\hfill \end{array}\right.$$ where A_j is the famous Adomian decomposition series. A detailed review of the ADM can be found (See Duan et al., 2012).

5. Employ the Pade-technique (Baker and Graves-Morris, 1996) to accelerate the convergence of u_n.

Remarks:

If a_i is a constant, the presented algorithm reduces to Tsay and Chen's LAPM. On the other hand, since the VIM allows the terms with variable coefficients as restricted variations, as a result, the modified VIM here is more flexible and general here.

This idea can also be extended to the fractional calculus of variations (Baleanu and Trujillo, 2008,2010). For the VIM in the fractional differential equations, the Lagrange multipliers can be determined readily from Laplace transform. Readers who feel interested in the method are referred to the recent development (Wu, 2012a, b, c).

Consider the following differential equations with a variable coefficient as an example

Considering the terms L[2tu] and L[u³] are restricted variations, take the classical variation operator on both sides of (9) $$\delta U_{n+1}(s)=\delta U_n(s)+\lambda (s^2-1)\delta U_n(s)$$ As a result, a Lagrange multiplier can be determined as

Substituting (10) into (9), one can obtain

With symbolic computation, we can derive the following approximate solutions

Now apply the Pade technique to u₈ and u₁₀ and denote the results by $u_8\left[\frac{10}{10}\right]$ and $u_{10}\left[\frac{16}{16}\right]\text{.}$ Define the residual value function as

Close

Figure 1

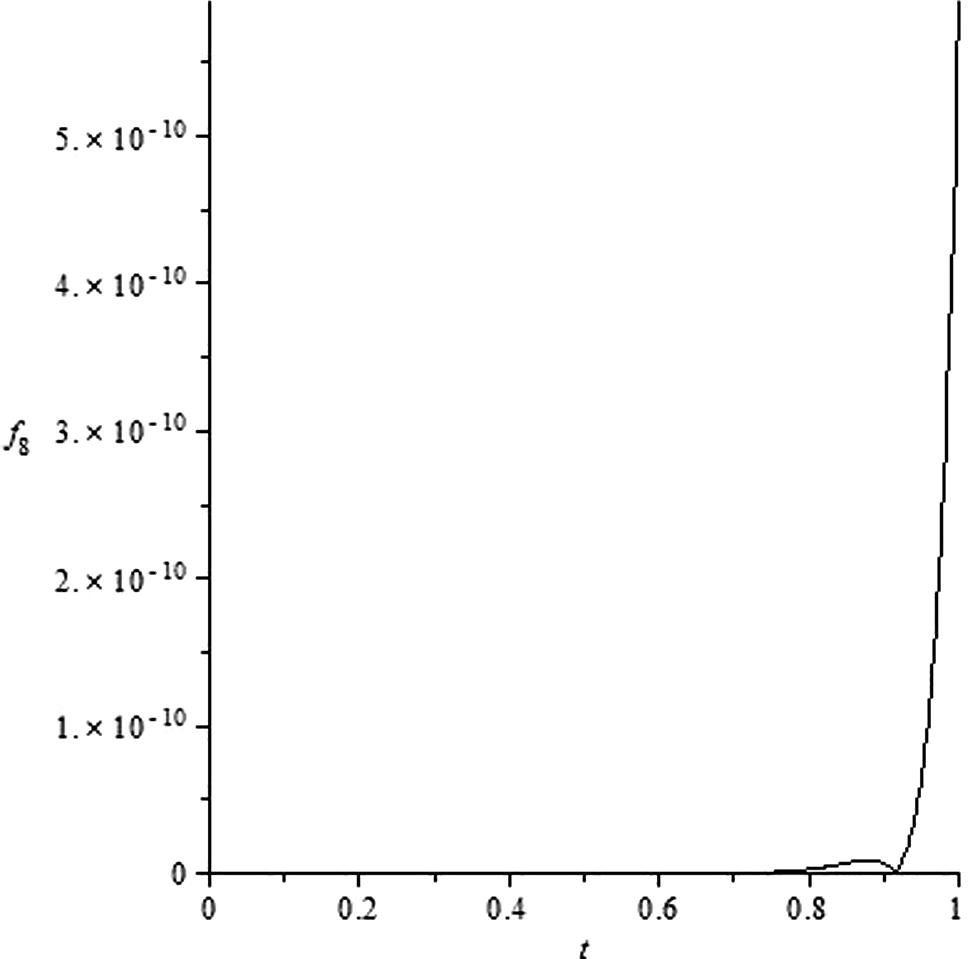
Curve of the residual value f₈.

Export to PPT

Close

Figure 2

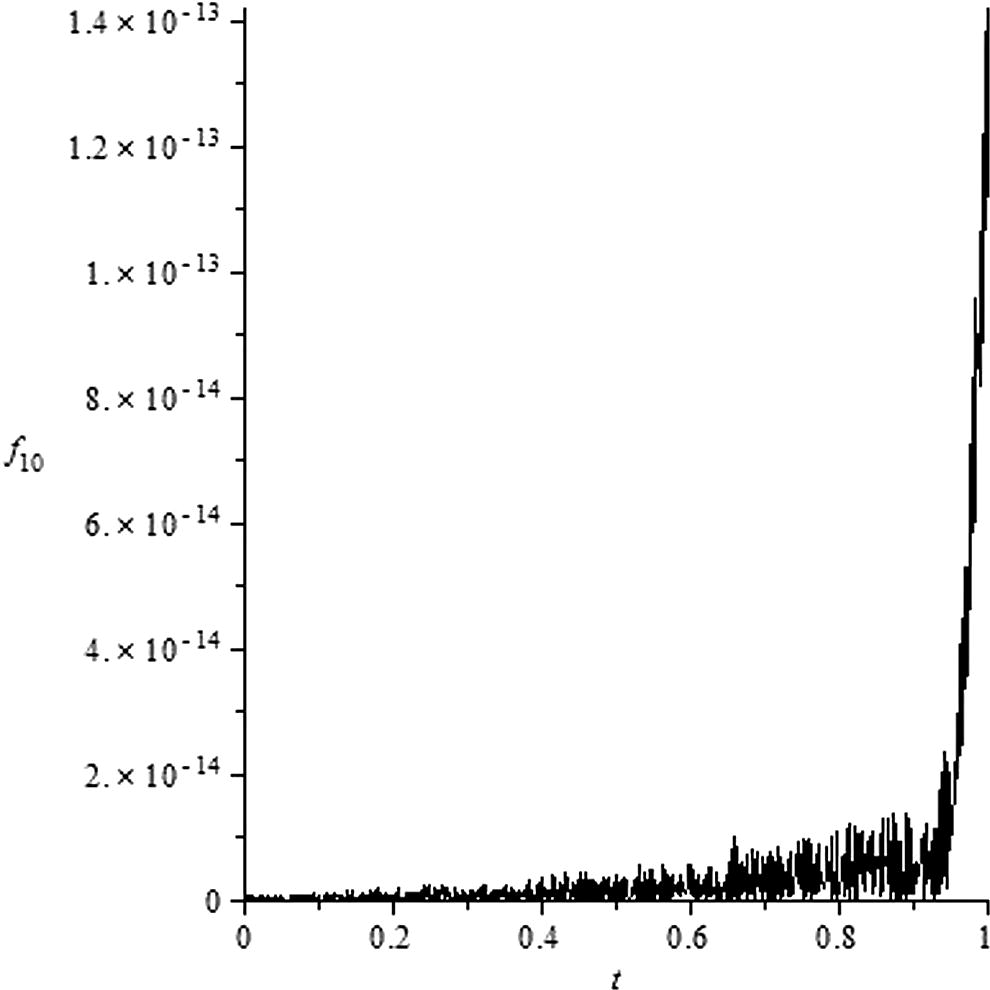
Curve of the residual value f₁₀.

Export to PPT

On the other hand, we also can have the following variational iteration formula for (7) $$\left\{\begin{array}{c}{u}_{n+1}(t)=u_0+L^{-1}[\lambda (s)L[(1+2t)u_n+u_n^3]]\text{,}\lambda (s)=-1/s^2\text{,}\hfill \\ u_0=t+t^2/2\hfill \end{array}\right.$$ if only the term $\frac{d^{2}u}{{\mathit{dt}}^2}$ is included in the calculus of variations.

4 Conclusions

The VIM has been extensively used for solving various differential equations. The critical step of the method is to identify the Lagrange multipliers through calculus of variations. In this study, the VIM is improved with Laplace transform and the Adomian series. Compared with the classical VIM, the modified version method has following merits: (a) the Lagrange multipliers can be readily obtained in a more straightforward way; (b) the initial iteration value can be determined universally; (c) The method is also powerful to solving differential equations with variable coefficients. The error analysis and higher order approximate solutions of the nonlinear oscillator illustrate the method's efficiencies and high accuracies.