Solution of the fractional epidemic model by homotopy analysis method

1 Introduction

Epidemiology is concerned with the spread of disease and its effect on people. This in itself encompasses a range of disciplines, from biology to sociology and philosophy, all of which are utilized to a better understanding and containing of the spread of infection.

One common epidemiological model is the SIR model for the spread of disease, which consists of a system of three differential equations that describe the changes in the number of susceptible, infected, and recovered individuals in a given population. This was introduced as far back as 1927 by Kermack and McKendrick (1927), and despite its simplicity, it is a good model for many infectious diseases. The SIR model is described by the following nonlinear differential system

The SIR model (1) consists of three variables: S(t) is the number of individuals in the susceptible compartment S at time t, in which all individuals are susceptible to the disease; I(t) is the number of individuals in the infected compartment I at time t, in which all individuals are infected by the disease and have infectivity; and R(t) is the number of individuals in the removed (recovered) compartment R at time t, in which all individuals are removed from the infected compartment. This model was made under the following three assumptions:

1. The disease spreads in a closed environment (no emigration and immigration), and there is no birth and death in the population, so the total population remains constant, N, i.e., S(t) + I(t) + R(t) = N.

2. An infected individual is introduced into the susceptible compartment, and contacts sufficient susceptibles at time t, so the number of new infected individuals per unit time is βS(t), where β is the transmission coefficient. The total number of newly infected is βS(t)I(t) at time t.

3. The number removed (recovered) from the infected compartment per unit time is γI(t) at time t, where γ is the rate constant for recovery, corresponding to a mean infection period of γ⁻¹. The recovered have permanent immunity.

In the SIR model considered here, we assume that there is a steady constant rate between susceptible and infectives and that a constant proportion of these constant results in transmission. Also, we ignore any subdivisions of the population by age, sex, mobility, or other factors, although such distinctions are obviously of importance. The reader is asked to refer to (Anderson and May, 1998; Bailey, 1975; Kelleci and Yıldırım, 2011; Murray, 1993; Yildirim and Cherruault, 2009; Yildirim and Koçak, 2011) in order to know more details about mathematical epidemiology, including its history and kinds, basics of SIR epidemic models, method of solutions, etc.

The differential equations with fractional order have recently proved to be valuable tools to the modeling of many real problems in different areas (Luchko and Gorenflo, 1998; Mainardi, 1997; Miller and Ross, 1993; Oldham and Spanier, 1974; Podlubny, 1999). This is because of the fact that the realistic modeling of a physical phenomenon does not depend only on the instant time, but also on the history of the previous time which can also be successfully achieved by using fractional calculus. For example, half-order derivatives and integrals proved to be more useful for the formulation of certain electrochemical problems than the classical models (Luchko and Gorenflo, 1998; Mainardi, 1997; Miller and Ross, 1993; Oldham and Spanier, 1974; Podlubny, 1999). Lately, a large amount of studies developed concerning the application of fractional differential equations in various applications in fluid mechanics, viscoelasticity, biology, physics, and engineering. An excellent account in the study of fractional differential equations can be found in (Kilbas et al., 2006; Lakshmikantham et al., 2009; Podlubny, 1999).

In this work, we study the mathematical behavior of the solution of a fractional SIR model as the order of the fractional derivative changes by extending the classical SIR model (1) to the following fractional SIR model

The reason for considering a fractional order system instead of its integer order counterpart is that the integer order system can be viewed as a special case from the fractional order system by putting the time-fractional order of the derivative equal to unity. Also, using fractional order differential equations can help us to reduce the errors arising from the neglected parameters in modeling real life phenomena (Luchko and Gorenflo, 1998; Miller and Ross, 1993; Podlubny, 1999). Furthermore, the fractional differential equations are innately reference to systems with memory, which stands in most biological systems. Since, the study found that fractional derivative was very suitable to describe long memory and hereditary properties of various materials and processes (Miller and Ross, 1993; Podlubny, 1999).

The HAM, which is proposed by Liao (1992), is effectively and easily used to solve some classes of nonlinear problems without linearization, perturbation, or discretization. In the last years, extensive work has been done using HAM, which provides analytical approximations for nonlinear equations. This method has been implemented in many branches of mathematics and engineering, such as nonlinear water waves (Liao and Cheung, 2003), unsteady boundary-layer flows (Liao, 2006), solitary waves with discontinuity (Wu and Liao, 2005), Klein–Gordon equation (Sun, 2005), fractional KdV-Burgers–Kuramoto equation (Song and Zhang, 2007), fractional nonlinear Riccati equation (Cang et al., 2009), coupled nonlinear diffusion reaction equations and the (2+1)-dimensional Nizhnik–Novikov Veselov system (El-Wakil and Abdou, 2010), Whitham–Broer–Kaup, coupled Korteweg–de Vries, and coupled Burger’s equations (El-Wakil and Abdou, 2008), nonlinear differential difference equations (Abdou, 2010), and others.

The objective of the present paper is to extend the applications of the HAM to provide symbolic approximate solutions for the fractional SIR model (3). As we will see later, choosing suitable values of the auxiliary parameter $\hslash$ will help us to adjust and control the convergence region of the series solution.

The organization of this paper is as follows: in the next section, we present some necessary definitions and preliminary results that will be used in our work. In Section 3, the basic idea of the HAM is introduced. In Section 4, we utilize the statement of the method for solving a fractional order SIR model by HAM. In Section 5, numerical results are given to illustrate the capability of HAM. In Section 6, the convergence of the HAM series solution is analyzed. The conclusion is given in the final part, Section 7.

2 Preliminaries

The material in this section is basic in some sense. For the reader’s convenience, we present some necessary definitions from fractional calculus theory and preliminary results. For the concept of fractional derivative, we will adopt Caputo’s definition, which is a modification of the Riemann–Liouville definition and has the advantage of dealing properly with initial value problems in which the initial conditions are given in terms of the field variables and their integer order, which is the case in most physical processes (Caputo, 1967; Luchko and Gorenflo, 1998; Mainardi, 1997; Miller and Ross, 1993; Oldham and Spanier, 1974; Podlubny, 1999).

Properties of the operator J^α can be found in (Caputo, 1967; Luchko and Gorenflo, 1998; Mainardi, 1997; Miller and Ross, 1993; Oldham and Spanier, 1974; Podlubny, 1999), we mention only the following: for f ∈ C_μ, μ ⩾ −1, α, β ⩾ 0, and γ ⩾ −1, we have $$\begin{array}{cc}\hfill & J^{\alpha }{J}^{\beta }f(x)=J^{\alpha +\beta }f(x)=J^{\beta }{J}^{\alpha }f(x)\text{,}\hfill \\ \hfill & J^{\alpha }{x}^{\gamma }=\frac{\mathrm{\Gamma }(\gamma +1)}{\mathrm{\Gamma }(\alpha +\gamma +1)}{x}^{\alpha +\gamma }\text{.}\hfill \end{array}$$

The Riemann–Liouville derivative has certain disadvantages when trying to model real-world phenomena with fractional differential equations. Therefore, we shall introduce a modified fractional differential operator $D_{\ast }^{\alpha }$ proposed by Caputo in his work on the theory of viscoelasticity (Caputo, 1967).

For mathematical properties of fractional derivatives and integrals, one can consult the mentioned references.

3 Basic idea of the HAM

The principles of the HAM and its applicability for various kinds of differential equations are given in (Cang et al., 2009; Liao, 1992, 1998, 2003, 2004, 2006; Liao and Cheung, 2003; Song and Zhang, 2007; Sun, 2005; Wu and Liao, 2005). For convenience of the reader, we will present a review of the HAM (Liao, 1992, 1998, 2003, 2004, 2006; Liao and Cheung, 2003; Wu and Liao, 2005) then we will implement the HAM to construct a symbolic approximate solution for the fractional SIR model (3) and (2). To achieve our goal, we consider the nonlinear differential equation

Liao (1992) constructs the so-called zeroth-order deformation equation

Thus, according to Eqs. (6) and (7), as q increasing from 0 to 1, the solution ϕ(t; q) varies continuously from the initial approximation y₀(t) to the exact solution y(t).

Define the so-called mth-order deformation derivatives

Assume that the auxiliary parameter ℏ, the auxiliary function H(t), the initial approximation y₀(t), and the auxiliary linear operator $\mathcal{L}$ are properly chosen so that the series (9) of ϕ(t; q) converges at q = 1. Then, we have under these assumptions the series solution $$y(t)=y_0(t)+\sum _{m=1}^{\infty }{y}_m(t)\text{.}$$

According to Eq. (8), the governing equation can be deduced from the zeroth-order deformation Eq. (5). Define the vector $${\overrightarrow{y}}_n=\{y_0(t)\text{,}{y}_1(t)\text{,}{y}_2(t)\text{,}\dots \text{,}{y}_n(t)\}\text{.}$$

Differentiating Eq. (5) m-times with respect to embedding parameter q, and then setting q = 0 and finally dividing them by m!, we have, using Eq. (8), the so-called mth-order deformation equation

For any given nonlinear operator N, the term $\mathcal{R}{y}_m({\overrightarrow{y}}_{m-1})$ can be easily expressed by Eq. (11). Thus, we can gain y₀(t), y₁(t), y₂(t), …, y_n(t) by means of solving the linear high-order deformation Eq. (10) one after the other in order. The mth-order approximation of y(t) is given by $$y(t)=\sum _{k=0}^{m-1}{y}_k(t)\text{.}$$

It should be emphasized that the so-called mth-order deformation Eq. (10) is linear, which can be easily solved by symbolic computation softwares such as Maple or Mathematica.

4 Solution of the fractional order SIR model by HAM

In this section, we employ our algorithm of the HAM to find out series solutions for the fractional SIR model of epidemics.

Let q ∈ [0, 1] be the so-called embedding parameter. The HAM is based on a kind of continuous mappings $$S(t)\to {\phi }_1(t\text{;}q)\text{,}I(t)\to {\phi }_2(t\text{;}q)\text{,}R(t)\to {\phi }_3(t\text{;}q)$$ such that, as the embedding parameter q increases from 0 to 1, φ_i(t; q), i = 1, 2, 3 varies from the initial approximation to the exact solution. To ensure this, choose such auxiliary linear operators ${\mathcal{L}}_i$ to be $D_{\ast }^{{\mu }_i}$ , where 0 < μ_i ⩽ 1, i = 1, 2, 3.

We define the nonlinear operators $$\begin{array}{c}{N}_1[{\phi }_1(t\text{;}q)]=D_{\ast }^{{\mu }_1}[{\phi }_1(t\text{;}q)]+\beta {\phi }_1(t\text{;}q){\phi }_2(t\text{;}q)\text{,}\hfill \\ N_2[{\phi }_2(t\text{;}q)]=D_{\ast }^{{\mu }_2}[{\phi }_2(t\text{;}q)]-\beta {\phi }_1(t\text{;}q){\phi }_2(t\text{;}q)+\gamma {\phi }_2(t\text{;}q)\text{,}\hfill \\ N_3[{\phi }_3(t\text{;}q)]=D_{\ast }^{{\mu }_3}[{\phi }_3(t\text{;}q)]-\gamma {\phi }_2(t\text{;}q)\text{.}\hfill \end{array}$$ Let h_i ≠ 0 and H_i(t) ≠ 0, i = 1, 2, 3, denote the so-called auxiliary parameter and auxiliary function, respectively. Using the embedding parameter q, we construct a family of equations $$\begin{array}{cc}\hfill & (1-q){\mathcal{L}}_1[{\phi }_1(t\text{;}q)-S_0(t)]=q{\hslash }_1{H}_1(t)N_1[{\phi }_1(t\text{;}q)]\text{,}\hfill \\ \hfill & (1-q){\mathcal{L}}_2[{\phi }_2(t\text{;}q)-I_0(t)]=q{\hslash }_2{H}_2(t)N_2[{\phi }_2(t\text{;}q)]\text{,}\hfill \\ \hfill & (1-q){\mathcal{L}}_3[{\phi }_3(t\text{;}q)-R_0(t)]=q{\hslash }_3{H}_3(t)N_3[{\phi }_3(t\text{;}q)]\text{,}\hfill \end{array}$$ subject to the initial conditions $${\phi }_1(0\text{;}q)=S_0(0)\text{,}{\phi }_2(0\text{;}q)=I_0(0)\text{,}{\phi }_3(0\text{;}q)=R_0(0)\text{.}$$

By Taylor’s theorem, we expand φ_i(t; q), i = 1, 2, 3 by a power series of the embedding parameter q as follows $$\begin{array}{cc}\hfill & {\phi }_1(t\text{;}q)=S_0(t)+\sum _{m=1}^{\infty }{S}_m(t)q^m\text{,}\hfill \\ \hfill & {\phi }_2(t\text{;}q)=I_0(t)+\sum _{m=1}^{\infty }{I}_m(t)q^m\text{,}\hfill \\ \hfill & {\phi }_3(t\text{;}q)=R_0(t)+\sum _{m=1}^{\infty }{R}_m(t)q^m\text{,}\hfill \end{array}$$ where $$\begin{array}{cc}\hfill & S_m(t)={\left.\frac{1}{m!}\frac{{\partial }^m{\phi }_1(t\text{;}q)}{\partial q^m}\right|}_{q=0}\text{,}\hfill \\ \hfill & I_m(t)={\left.\frac{1}{m!}\frac{{\partial }^m{\phi }_2(t\text{;}q)}{\partial q^m}\right|}_{q=0}\text{,}\hfill \\ \hfill & R_m(t)={\left.\frac{1}{m!}\frac{{\partial }^m{\phi }_3(t\text{;}q)}{\partial q^m}\right|}_{q=0}\text{.}\hfill \end{array}$$ Then at q = 1, the series becomes

For simplicity, we can choose the auxiliary functions as H_i(t) = 1, i = 1, 2, 3 and take ${\mathcal{L}}_i=D_{\ast }^{{\mu }_i}\text{,}i=1\text{,}2\text{,}3$ , then the right inverse of $D_{\ast }^{{\mu }_i}$ will be $J^{{\mu }_i}$ ; the Riemann–Liouville fractional integral operator. Hence, the mth-order deformation Eq. (13) for m ⩾ 1 becomes $$\begin{array}{cc}\hfill & S_m(t)={\chi }_m{S}_{m-1}(t)+{\hslash }_1{J}^{{\mu }_1}[\mathcal{R}{S}_m({\overrightarrow{S}}_{m-1}(t))]\text{,}\hfill \\ \hfill & I_m(t)={\chi }_m{I}_{m-1}(t)+{\hslash }_2{J}^{{\mu }_2}[\mathcal{R}{I}_m({\overrightarrow{I}}_{m-1}(t))]\text{,}\hfill \\ \hfill & R_m(t)={\chi }_m{R}_{m-1}(t)+{\hslash }_3{J}^{{\mu }_3}[\mathcal{R}{R}_m({\overrightarrow{R}}_{m-1}(t))]\text{.}\hfill \end{array}$$ If we choose S₀(t) = S(0) = N_S, I₀(t) = I(0) = N_I, and R₀(t) = R(0) = N_R as initial guess approximations of S(t), I(t), and R(t), respectively, then two terms approximations for S(t), I(t), and R(t) are calculated and presented below $$\begin{array}{cc}\hfill & S_1=t\beta {\hslash }_1{N}_I{N}_S\text{,}\hfill \\ \hfill & S_2=t\beta {\hslash }_1{N}_I{N}_S+\frac{t^2\beta {\hslash }_1{N}_I{N}_S(2t^{-{\mu }_1}{\hslash }_1+(\beta {\hslash }_1{N}_I+{\hslash }_2(\gamma -\beta N_S))\mathrm{\Gamma }[3-{\mu }_1])}{2\mathrm{\Gamma }[3-{\mu }_1]}\text{,}\hfill \\ \hfill & I_1=t{\hslash }_2(\gamma N_I-\beta N_I{N}_S)\text{,}\hfill \\ \hfill & I_2=t{\hslash }_2(\gamma N_I-\beta N_I{N}_S)-\frac{t^{2-{\mu }_2}{\hslash }_2{N}_I}{2\mathrm{\Gamma }[3-{\mu }_2]}\left\{-t^{{\mu }_2}{\beta }^2{\hslash }_2{N}_S^2\mathrm{\Gamma }[3-{\mu }_2]-\gamma {\hslash }_2(2+t^{{\mu }_2}\gamma \mathrm{\Gamma }[3-{\mu }_2])+\beta N_S(t^{{\mu }_2}\beta {\hslash }_1{N}_I\mathrm{\Gamma }[3-{\mu }_2]+2{\hslash }_2(1+t^{{\mu }_2}\gamma \mathrm{\Gamma }[3-{\mu }_2]))\right\}\text{,}\hfill \\ \hfill & R_1=-t\gamma {\hslash }_3{N}_I\text{,}\hfill \\ \hfill & R_2=-t\gamma {\hslash }_3{N}_I+\frac{1}{2}{t}^2\gamma {\hslash }_3{N}_I\left(-\gamma {\hslash }_2+\beta {\hslash }_2{N}_S-\frac{2t^{-{\mu }_3}{\hslash }_3}{\mathrm{\Gamma }[3-{\mu }_3]}\right)\text{.}\hfill \end{array}$$

Finally, we approximate the solution S(t), I(t), and R(t) of the model (3) and (2) by the kth-truncated series

We mention here that, if we set the auxiliary parameters ℏ₁ = ℏ₂ = ℏ₃ = −1 and μ₁ = μ₂ = μ₃ = 1, then the HAM solution is the same as the Adomian decomposition solution obtained in (Biazar, 2006) and the homotopy perturbation solution obtained in (Rafei et al., 2007). Through this paper, we fixed the auxiliary parameters ℏ₂ = ℏ₃ = −1.

5 Numerical results

The HAM provides an analytical approximate solution in terms of an infinite power series. However, there is a practical need to evaluate this solution, and to obtain numerical values from the infinite power series. The consequent series truncation and the practical procedure are conducted to accomplish this task.

For numerical results, the following values, for parameters, are considered (Biazar, 2006):

To consider the behavior of solution for different values of μ_i, i = 1, 2, 3, we will take advantage of the explicit formula (14) available for 0 < μ_i ⩽ 1, i = 1,2,3, and consider the following two special cases:

6 Convergence of the series solution

The HAM yields rapidly convergent series solution by using a few iterations. For the convergence of the HAM, the reader is referred to Liao (2003).

According to Rashidi et al. (2011), it is to be noted that the series solution contains the auxiliary parameter ℏ₁ which provides a simple way to adjust and control the convergence of the series solution. In fact, it is very important to ensure that the series Eq. (12) are convergent. To this end, we have plotted ℏ₁-curves of S′(0), I′(0), and R′(0) by seventh order approximation of the HAM in Figs. 1–3, respectively, for μ₁ = μ₂ = μ₃ = 1 and μ₁ = μ₂ = μ₃ = 0.75.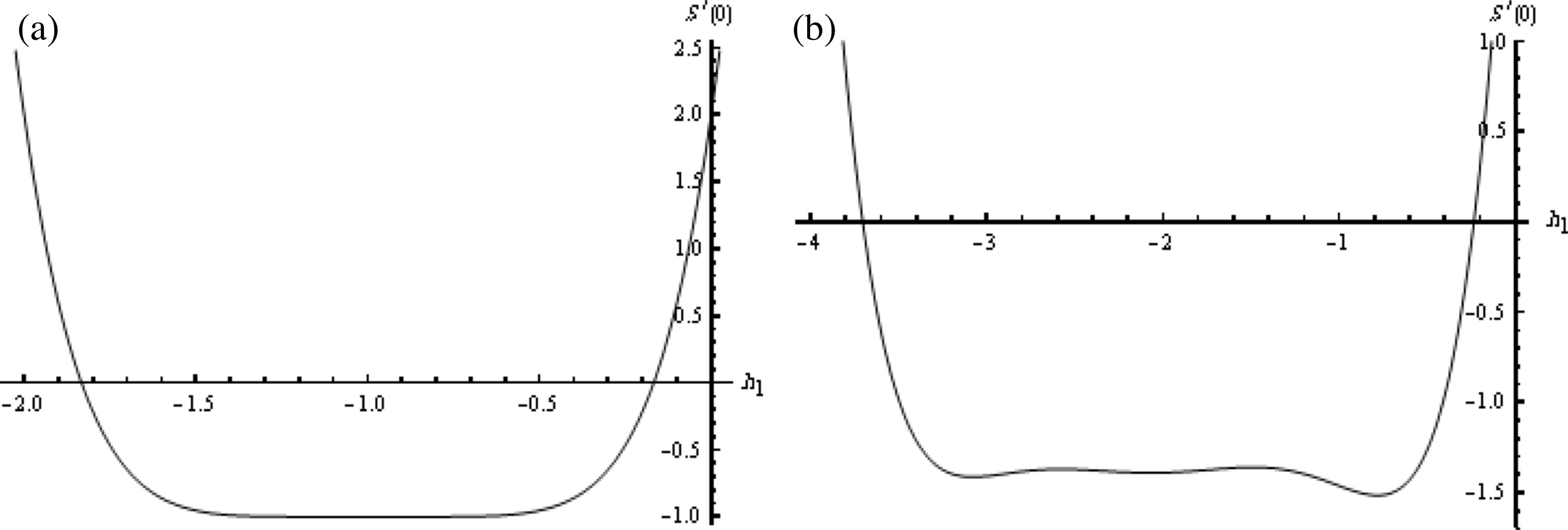

Close

Figure 1

The ℏ₁-curve of S′(0) obtained by the seventh order approximation of the HAM: (a) when μ₁ = μ₂ = μ₃ = 1; (b) when μ₁ = μ₂ = μ₃ = 0.75.

Export to PPT

Close

Figure 2

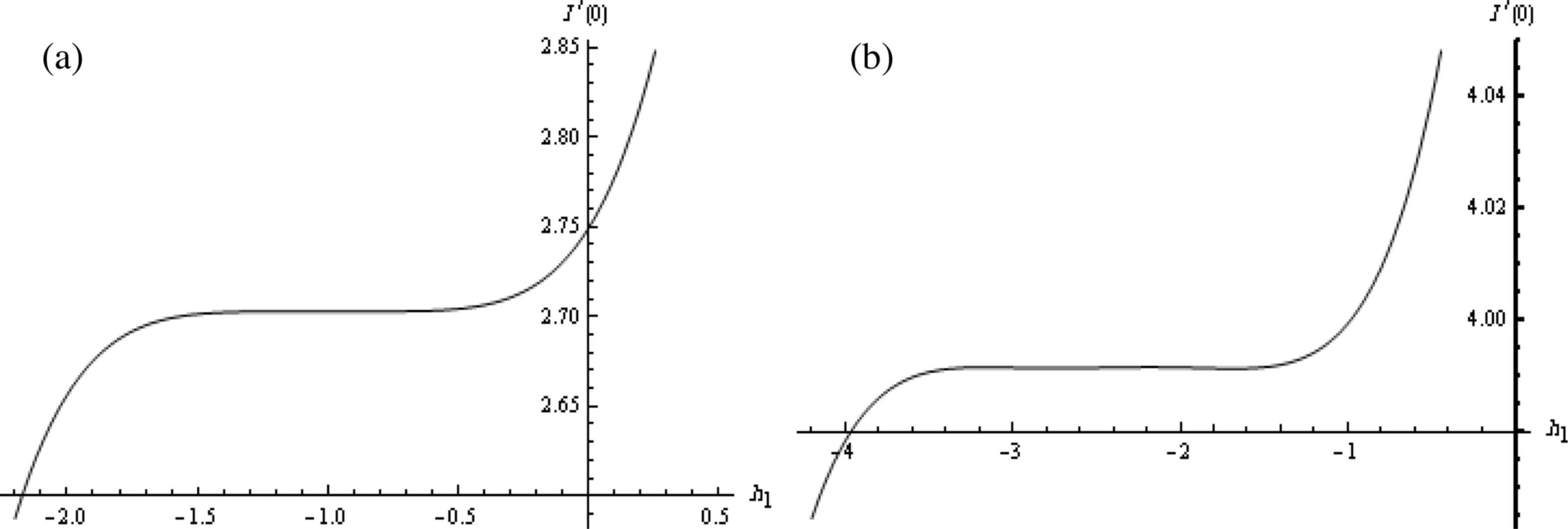
The ℏ₁-curve of I′(0) obtained by the seventh order approximation of the HAM: (a) when μ₁ = μ₂ = μ₃ = 1; (b) when μ₁ = μ₂ = μ₃ = 0.75.

Export to PPT

Close

Figure 3

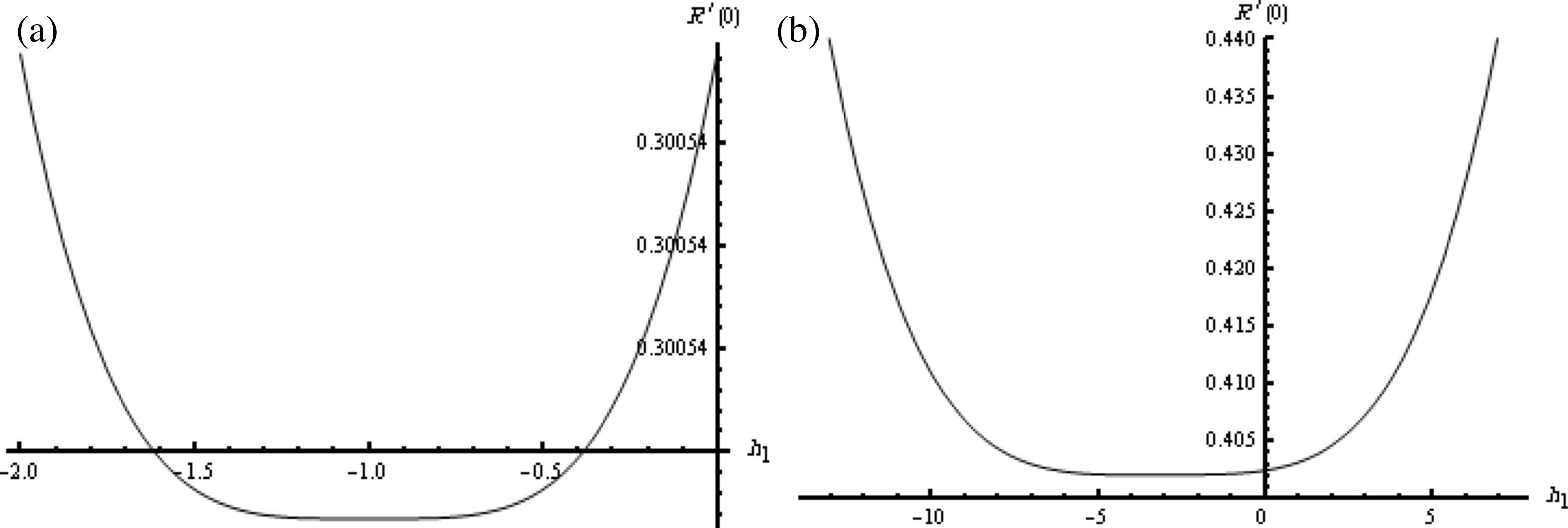
The ℏ₁-curve of R′(0) obtained by the seventh order approximation of the HAM: (a) when μ₁ = μ₂ = μ₃ = 1; (b) when μ₁ = μ₂ = μ₃ = 0.75.

Export to PPT

Again, according to these ℏ₁-curves, it is easy to discover the valid region of ℏ₁ which corresponds to the line segment nearly parallel to the horizontal axis. These valid regions have been listed in Table 1. Furthermore, these valid regions ensure us the convergence of the obtained series.

These results are plotted in Figs. 4–6, respectively, at the end points of the valid region given in Table 1 together with ℏ₁ = −1 for the three components S(t), I(t), and R(t), respectively. As the plots show, while the number of susceptibles increases, the population of who are infective decreases in the period of the epidemic. Meanwhile, the number of immune population increases, but the size of the population over the period of the epidemic is constant.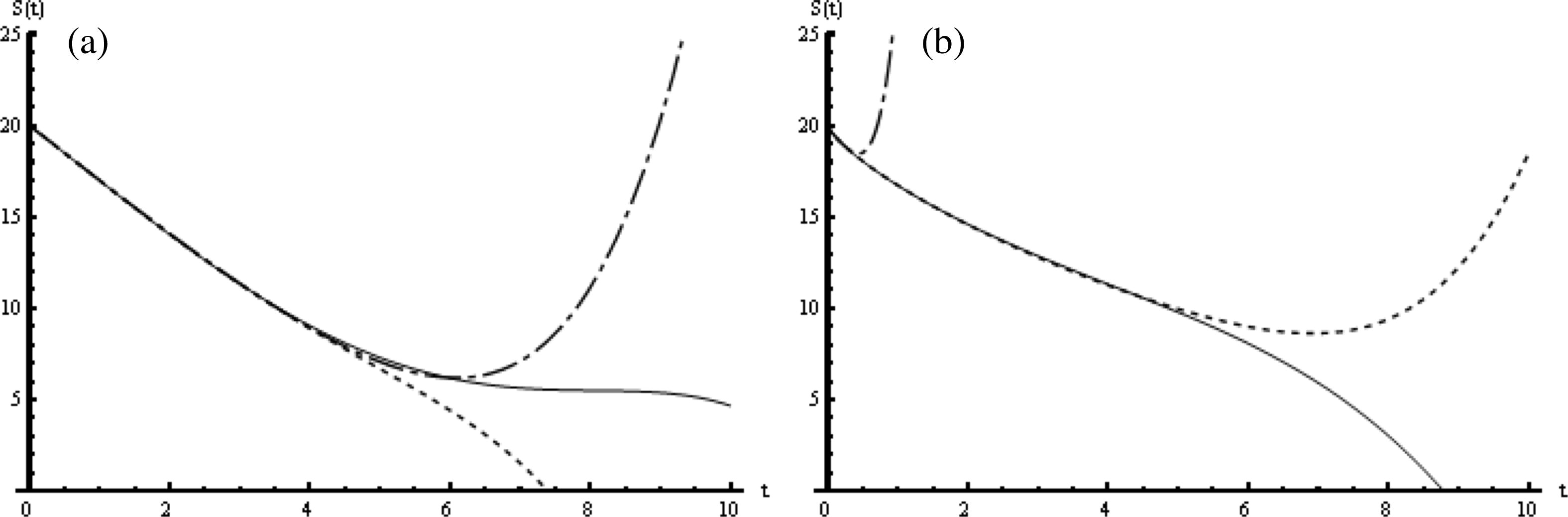

Close

Figure 4

The HAM solution of S(t): (a) when μ₁ = μ₂ = μ₃ = 1; dash-dotted line: ℏ₁ = −1.4, dotted line: ℏ₁ = −1, solid line: ℏ₁ = −0.6. (b) when μ₁ = μ₂ = μ₃ = 0.75; dash-dotted line: ℏ₁ = −2.7, dotted line: ℏ₁ = −1, solid line: ℏ₁ = −0.8.

Export to PPT

Close

Figure 5

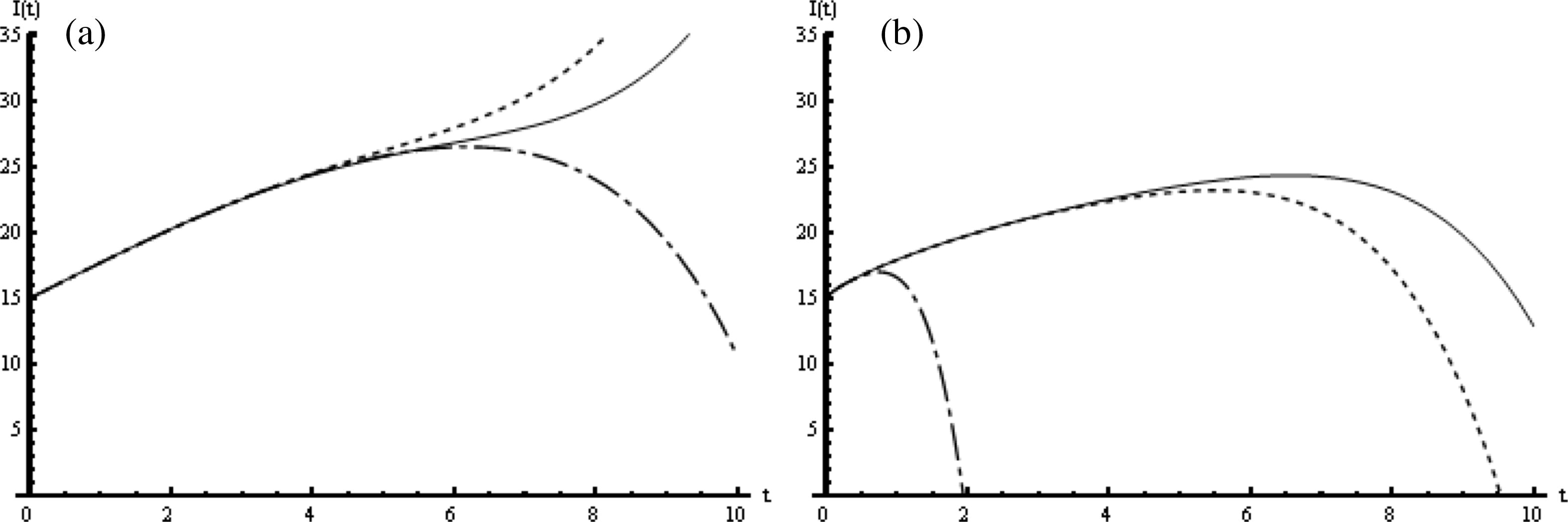
The HAM solution of I(t): (a) when μ₁ = μ₂ = μ₃ = 1; dash-dotted line: ℏ₁ = −1.4, dotted line: ℏ₁ = −1, solid line: ℏ₁ = −0.5. (b) when μ₁ = μ₂ = μ₃ = 0.75; dash-dotted line: ℏ₁ = −3.2, dotted line: ℏ₁ = −1, solid line: ℏ₁ = −1.2.

Export to PPT

Close

Figure 6

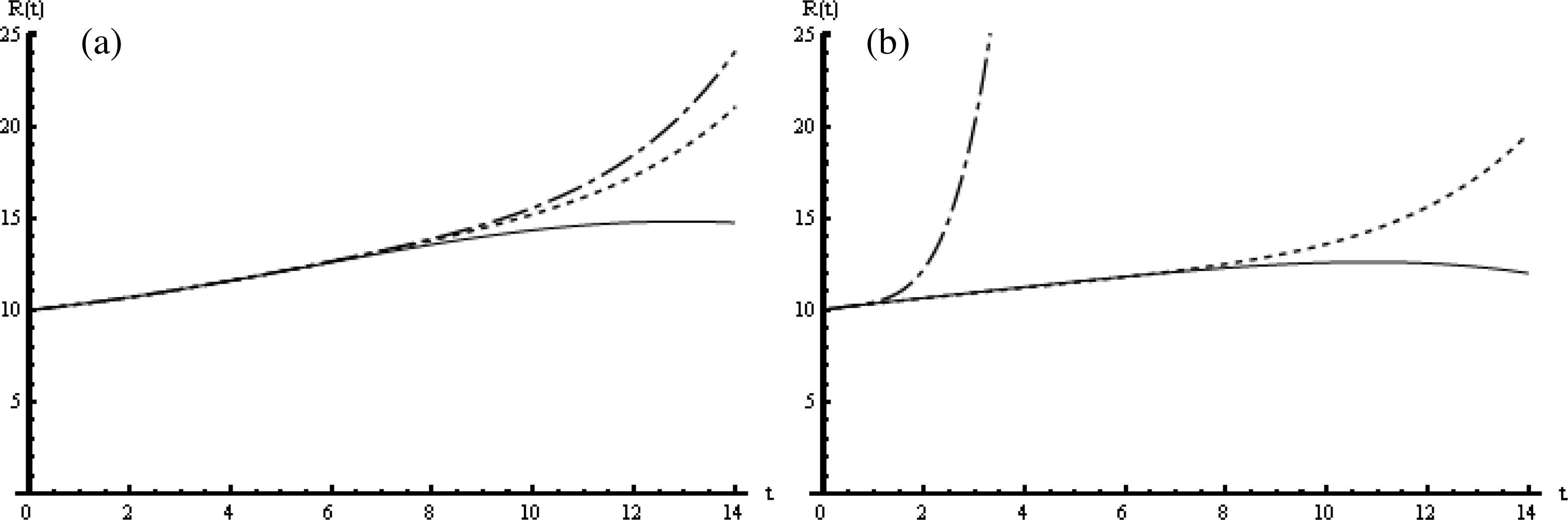
The HAM solution of R(t): (a) when μ₁ = μ₂ = μ₃ = 1; dash-dotted line: ℏ₁ = −1.2, dotted line: ℏ₁ = −1, solid line: ℏ₁ = −0.7 (b) when μ₁ = μ₂ = μ₃ = 0.75; dash-dotted line: ℏ₁ = −5, dotted line: ℏ₁ = −1, solid line: ℏ₁ = −0.2.

Export to PPT

To determine the optimal values of ℏ₁ in an interval [t₀, t₁], an error analysis is performed. We substitute the approximations ψ_S,7(t), ψ_I,7(t), and ψ_R,7(t) in Case 1 and Case 2 into Eq. (3) and obtain the residual functions; ER_S, ER_I, and ER_R as follows $$\begin{array}{cc}\hfill & {\mathit{ER}}_S(t\text{,}{\hslash }_1)=D_{\ast }^{{\mu }_1}[{\psi }_{S\text{,}k}(t)]+\beta {\psi }_{S\text{,}k}(t){\psi }_{I\text{,}k}(t)\text{,}\hfill \\ \hfill & {\mathit{ER}}_I(t\text{,}{\hslash }_1)=D_{\ast }^{{\mu }_2}[{\psi }_{I\text{,}k}(t)]-\beta {\psi }_{S\text{,}k}(t){\psi }_{I\text{,}k}(t)+\gamma {\psi }_{I\text{,}k}(t)\text{,}\hfill \\ \hfill & {\mathit{ER}}_R(t\text{,}{\hslash }_1)=D_{\ast }^{{\mu }_3}[{\psi }_{R\text{,}k}(t)]-\gamma {\psi }_{I\text{,}k}(t)\text{.}\hfill \end{array}$$ Following Liao (2010), we define the square residual error for approximation solutions on the interval [t₀, t₁] as $$\begin{array}{cc}\hfill & {\mathit{SER}}_S({\hslash }_1)={\int }_{t_0}^{t_1}{[{\mathit{ER}}_S(t\text{,}{\hslash }_1)]}^2\mathit{dt}\text{,}\hfill \\ \hfill & {\mathit{SER}}_I({\hslash }_1)={\int }_{t_0}^{t_1}{[{\mathit{ER}}_I(t\text{,}{\hslash }_1)]}^2\mathit{dt}\text{,}\hfill \\ \hfill & {\mathit{SER}}_R({\hslash }_1)={\int }_{t_0}^{t_1}{[{\mathit{ER}}_R(t\text{,}{\hslash }_1)]}^2\mathit{dt}\text{.}\hfill \end{array}$$

By using the first derivative test, we can easily determine the values of ℏ₁ for which the SER_S, SER_I, and SER_R are minimum.

In Niu and Wang (2010), several methods have been introduced to find the optimal value of ℏ₁. In Tables 2 and 3, the optimal values of ℏ₁ for the two previous cases are tabulated.

In Tables 4 and 5, the absolute errors ER_S, ER_I, and ER_R have been calculated for the various t in]0, 1]. From the tables, it can be seen that the HAM provides us with the accurate approximate solution for the fractional SIR model (3) and (2).

7 Conclusion

In this paper, the HAM has successfully been applied to finding the approximate solution of fractional SIR model. The present scheme shows importance of choice of convergence control parameter to guarantee the convergence of the solutions. Moreover, higher accuracy can be achieved using HAM by evaluating more components of the solution. In the near future, we intend to make more researches as continuation to this work. One of these researches is: application of HAM to solve fractional SEIR model.