Translate this page into:
A software for the one-dimensional cutting stock problem
*Corresponding author. Tel.: +90 5359233879 murat.ersen.berberler@ege.edu.tr (Murat Erşen Berberler),
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Abstract
In this paper, one-dimensional cutting stock problem is taken into consideration and a new heuristic algorithm is proposed to solve the problem. In this proposed algorithm, a new dynamic programming algorithm is applied for packing each of the bins. The algorithm is coded with Delphi and then by computational experiments with the real-life constraint optimization problems, and the obtained results are compared with the other one-dimensional cutting stock commercial packages. The computational experiments show the efficiency of the algorithm.
Keywords
Cutting stock problem
Bin packing problem
Dynamic programming
Heuristic algorithm
Packet program
1 Introduction
Cutting stock problems (CSPs) exist during the manufacturing processes of many products in the processing and manufacturing industries, such as the aluminum windows/doors frame manufacturing industry, the timber industry and the shipbuilding industry, and have become an important aspect of these industries. To ensure that orders are delivered efficiently, the management usually utilizes various manufacturing methods to minimize production costs. Therefore, the cutting process, which is common in these industries, has been considered from time to time as one that needs to be optimized. Reducing trim loss is one of the major goals during cutting processes and is also the main goal of 1D-CSP. Thus, the problem considered in this paper is to find a cutting plan that would minimize the waste of material when a set of orders that are different in length and quantity is to be cut from a pack of stocks with constant length (Yang et al., 2006).
The 1D-CSP (or CSP) in Fig. 1 is defined by the following data:
, where L denotes the length of each stock piece,
denotes the number of smaller piece types and for each type
,
is the piece length, and
is the order demand. In a cutting plan, we must obtain the required set of pieces from the available stock lengths. The objective is to minimize the number of used stock lengths or, equivalently, trim loss (waste). In a real-life cutting process there are additional criteria, e.g., the number of different cutting patterns (setups) and open stacks.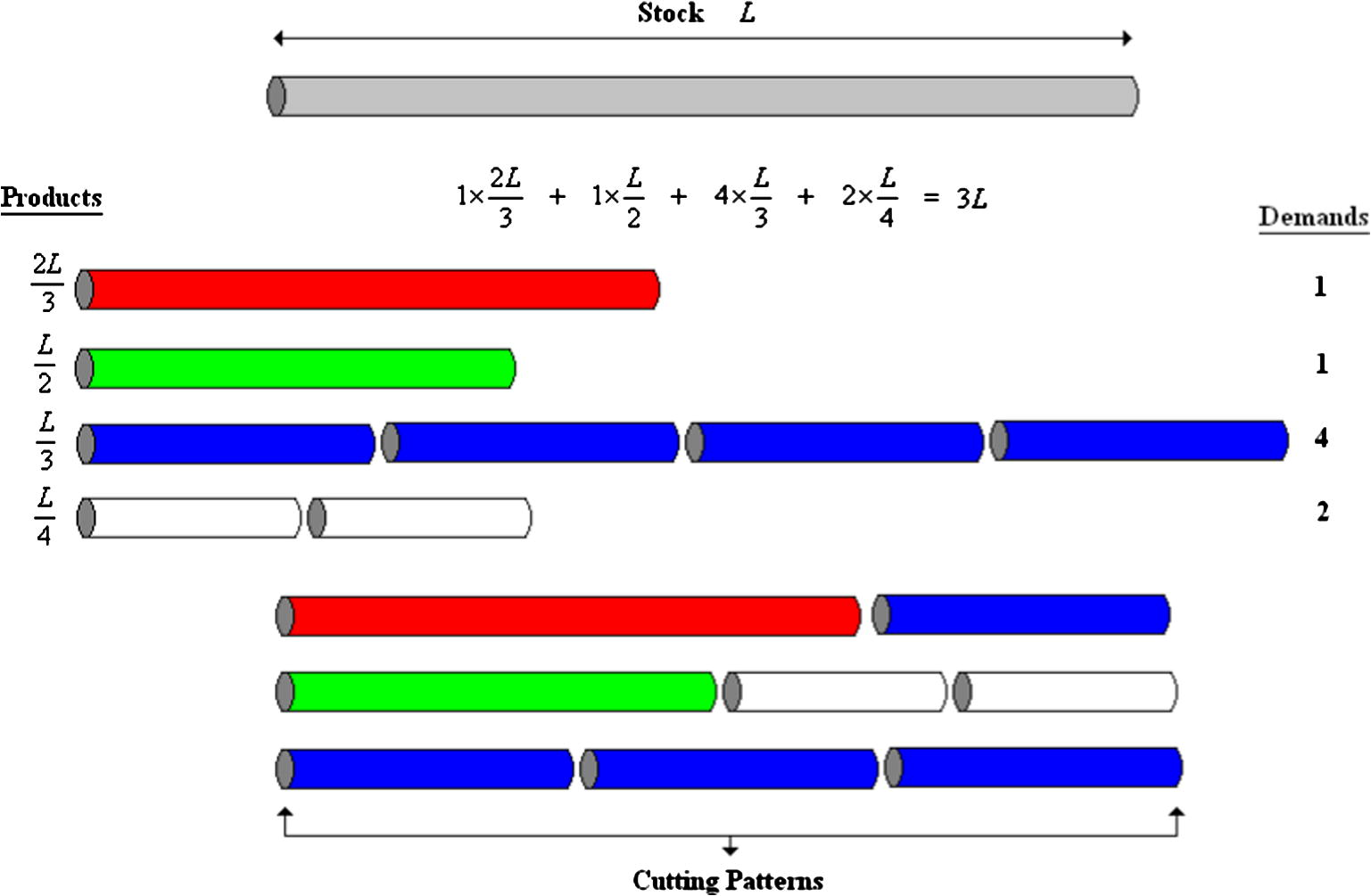
One-dimensional cutting stock problem with one stock type.
A special case in which the set of small objects is such that only one item of each product type is ordered, i.e., (sometimes also when are very small), is known as the Bin-Packing Problem (BPP, 1D-BPP). This special case, having a smaller overall number of items, is more suitable for pure combinatorial solution approaches (Belov, 2003).
We suppose that there are a definite number of bins of the same capacity and many packages of different shapes. BPP is the problem of placing all the packages in a minimum number of bins without exceeding the capacity. It has many application fields such as scheduling television commercials of different lengths by 1 min time interval or cutting timbers, used for building, into pieces of different lengths (Gilmore and Gomory, 1961; Gilmore et al., 1963), loading trucks, storage problem and budget planning. As it is well known, the BPP is strong NP-complete, when formulated as a decision problem. As an optimization problem, bin packing is NP-hard (Garey and Johnson, 1979). Many heuristic algorithms are known for the solution of this problem in the literature (Kellerer et al., 2004; Martello and Toth, 1990). To solve the bin-packing problem, a dynamic programming-based algorithm is proposed in this study.
We give a new mathematical model of the CSP in the next section.
2 A new mathematical model of the CSP
This model differs from the model existing in the literature by accepting the inputs as the classified equal length items. One of the advantages of this difference is that the length of the array which includes the items shortens. The other is that there is no computational cost of classifying the items.
n items
and
bins are given,
= weight of item
= number of item
(demand)
c = capacity of each bin
Solving the problem, a heuristic algorithm based on dynamic programming is developed. In this algorithm, for loading each of the bins, a novel dynamic programming algorithm is used. In the literature, this sub-problem is called Subset-Sum Problem (SSP).
3 A new algorithm for the CSP
The terms of BPP are used here to simplify the expression of the algorithm of CSP.
CSP (BPP) algorithm:
BPP1: and are entered. The entries are the weight of the items, the demands and the capacity of a bin.
BPP2: Number of bins is set to zero, here indicates the number of bins used.
BPP3: If . (If the sum of the demands of whole items is smaller than the capacity (of a bin), then go to step BPP10.)
BPP4: Considering the data entry above, the exact solution is found by using the below dynamic programming algorithm for packing a bin.
The solution is denoted by . Here, shows how many item are placed into the bin.
BPP5: is determined. The use-rate of the most used item is determined in the solution vector which is found at the previous step. The rates that are faced are not taken into consideration.
BPP6: This process is repeated for all the cases in which the bin can be packed completely full, the problem, taking , is resolved for a bin. Among these solutions, the ones in which the large sized items used are more preferred. Assume that the solution below is chosen eventually:
BPP7: is found and the amount of of bins is loaded considering solution (*).
The rates that are faced are not taken into consideration.
BPP8: The demand of item is updated by decreasing the amount of it being used.
BPP9: , go to BPP3.
BPP10: END.
The details of the algorithm are given above and the flow chart of the algorithm is seen in Fig. 2.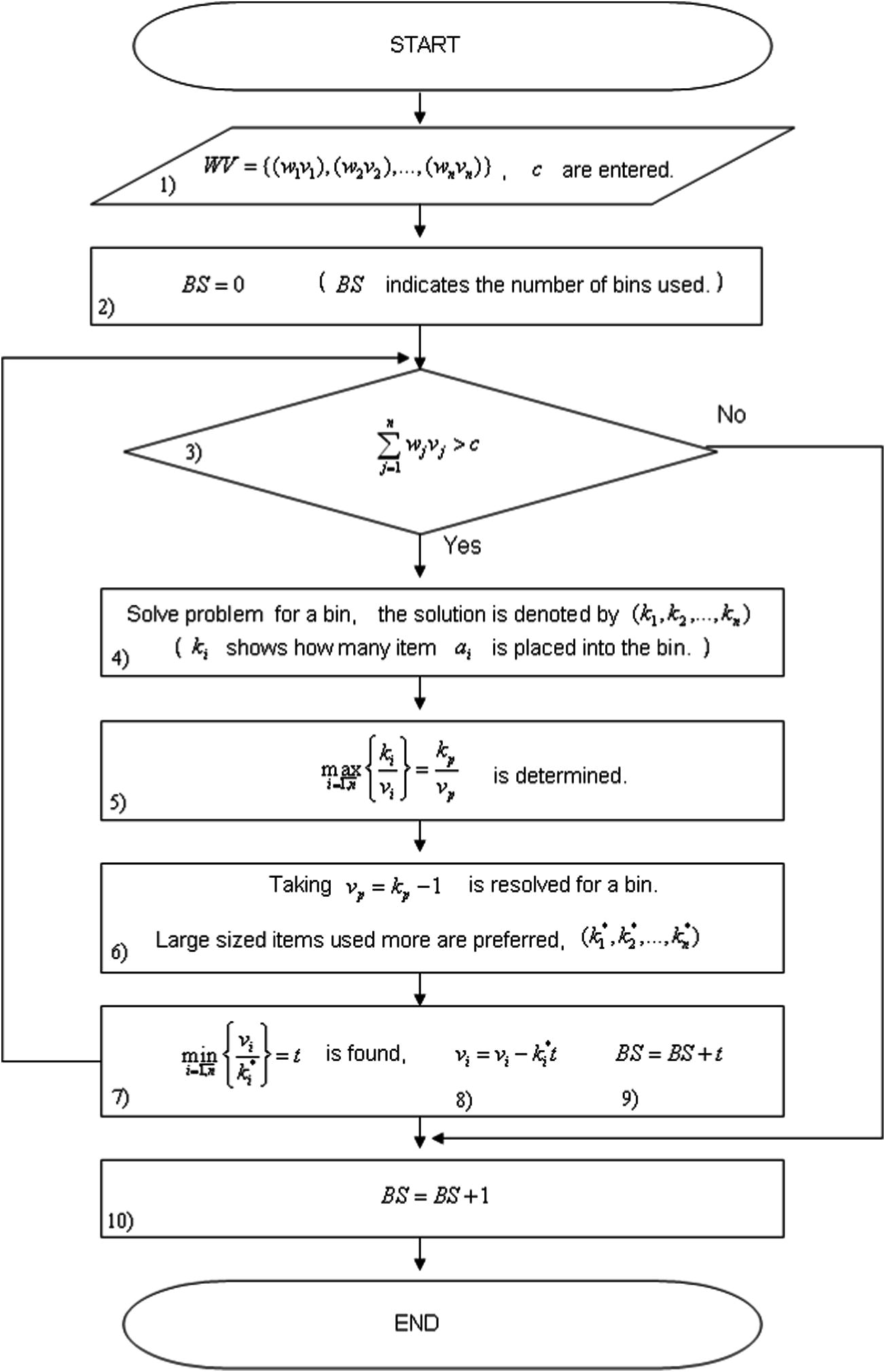
The flow chart of the algorithm CSP.
4 Software and computational experiments
MKA Yazılım ve Mühendislik Hizmetleri Ltd. Şti.1 has motivated us to perform this software. MKA was founded in 2005 May and the aim of the firm is to be a specialist in engineering software. One of the computer software products of MKA is the ÇelikProIV which is used for the planar design of industrial structures, for their resolving, for preparing their quantity take-off and for their graphics. The demand of MKA is to embed the ÇelikProIV into the module CSP. The explanation (claim) of them is that the commercial packages in the market are more expensive and they take much more CPU time. Thus, the detailed problem analysis, mathematical model and the algorithm based on this model are all taken into account and finally a software called bbkp is developed [bbkp]. Since the aim of the study is based on a modulation, the user interface was not paid much attention. Here a dynamic library DLL is given to MKA.
But, bbkp, as it stands, has been exhibited in the project markets and paid great attention by the firms of the manufacturing sector (Nuriyev et al., 2008, 2007).
The computational experiments are based on the higher difficulty degree real-life constraint optimization problems that are chosen from MKA. The two problems called PI and PII are shown in Table 1. The length of the stick is 6000 mm for each of the two problems. The notation in Section 3 is used to understand the terms of the problems easily.
j
PI
PII
wj
vj
wj
vj
1
992
10
1304
6
2
806
20
978
12
3
771
5
843
18
4
604
12
702
8
5
496
8
661
10
6
200
30
504
4
7
120
20
440
12
8
44
18
319
4
9
230
10
10
175
8
For benchmarking of the problems of MKA, we used the commercial 1D cutting stock software that is available via internet. The software packages were searched using the key word “one-dimensional cutting stock program” at www.google.com. The results were scanned to retrieve applicable software. Only five packages were chosen to have executable demo versions available. The names of the packages and their web sites are listed at the end of the references [A], [B], [C], [D], [E].
bbkp gives optimum results and it can be seen from Tables 2 and 3 for PI and PII. On the other hand PI has optimum result for packages B and C and PII has optimum result packages B, C and E. These results show that the software is as well designed as the other commercial packages in terms of the solution quality.
wj
j/bi
1
2
3
4
5
6
7
8
9
Σvj
bbkp
992
1
2
2
2
4
10
806
2
2
2
2
6
6
2
20
771
3
4
1
5
604
4
1
1
1
1
1
6
1
12
496
5
2
3
3
8
200
6
9
9
9
1
1
1
30
120
7
7
3
3
6
1
20
44
8
1
16
1
18
6000
6000
6000
6000
6000
6000
6000
6000
2303
100.00
100.00
100.00
100.00
100.00
100.00
100.00
100.00
38.38
100.00
A
992
1
1
1
4
4
10
806
2
2
2
5
5
3
3
20
771
3
1
1
1
1
1
5
604
4
1
1
3
3
2
2
12
496
5
4
4
8
200
6
9
9
6
6
30
120
7
6
6
8
20
44
8
1
1
1
1
14
18
6000
6000
5994
5994
5993
5993
5991
5991
2347
100.00
100.00
99.90
99.90
99.88
99.88
99.85
99.85
39.12
99.91
B
992
1
3
2
2
2
1
10
806
2
2
1
1
6
6
4
20
771
3
2
2
1
5
604
4
2
2
1
1
4
2
12
496
5
4
4
8
200
6
4
1
1
1
19
4
30
120
7
2
2
2
3
3
3
5
20
44
8
5
5
5
3
18
6000
6000
6000
6000
6000
6000
6000
6000
2303
100.00
100.00
100.00
100.00
100.00
100.00
100.00
100.00
38.38
100.00
C
992
1
3
3
3
1
10
806
2
2
2
2
2
6
6
20
771
3
4
1
5
604
4
1
1
1
1
3
5
12
496
5
6
1
1
8
200
6
3
3
3
5
5
2
8
1
30
120
7
1
1
1
6
1
1
1
7
1
20
44
8
2
2
2
2
1
1
2
1
5
18
6000
6000
6000
6000
6000
6000
6000
6000
2303
100.00
100.00
100.00
100.00
100.00
100.00
100.00
100.00
38.38
100.00
D
992
1
4
4
2
10
806
2
6
5
5
4
20
771
3
4
1
5
604
4
2
2
4
2
2
12
496
5
1
7
8
200
6
5
2
2
8
8
2
3
30
120
7
1
3
3
1
1
6
1
4
20
44
8
1
7
7
1
2
18
6000
5998
5998
5996
5996
5996
5972
5971
2376
100.00
99.97
99.97
99.93
99.93
99.93
99.53
99.52
39.60
99.85
E
992
1
2
2
1
1
1
1
1
1
10
806
2
1
1
3
3
3
3
3
3
20
771
3
2
2
1
5
604
4
2
2
2
2
2
2
12
496
5
1
1
1
1
1
1
1
1
8
200
6
4
4
3
3
3
3
3
3
4
30
120
7
2
2
2
2
2
2
2
2
4
20
44
8
3
3
1
1
1
1
1
1
6
18
6000
6000
5998
5998
5998
5998
5998
5998
2315
100.00
100.00
99.97
99.97
99.97
99.97
99.97
99.97
38.58
99.98
wj
j/bi
1
2
3
4
5
6
7
8
9
10
Σvj
bbkp
1304
1
1
1
1
1
1
1
6
978
2
3
3
3
3
12
843
3
5
4
3
6
18
702
4
4
4
8
661
5
2
2
2
2
2
10
504
6
2
2
4
440
7
2
2
1
1
1
1
4
12
319
8
2
2
4
230
9
7
1
2
10
175
10
1
6
1
8
6000
6000
6000
6000
6000
6000
6000
6000
5999
5233
100.00
100.00
100.00
100.00
100.00
100.00
100.00
100.00
99.98
87.22
100.00
A
1304
1
1
1
1
1
2
6
978
2
3
3
3
3
12
843
3
4
4
4
4
2
18
702
4
2
2
2
2
8
661
5
2
2
2
2
2
10
504
6
3
1
4
440
7
2
2
2
2
4
12
319
8
1
1
1
1
4
230
9
2
2
2
2
2
10
175
10
1
7
8
5998
5998
5998
5998
5997
5997
5997
5997
5981
5271
99.97
99.97
99.97
99.97
99.95
99.95
99.95
99.95
99.68
87.85
99.93
B
1304
1
1
1
1
1
1
1
6
978
2
2
5
5
12
843
3
3
3
3
3
2
2
2
18
702
4
4
4
8
661
5
2
2
2
2
1
1
10
504
6
4
4
440
7
1
1
1
1
2
2
1
1
2
12
319
8
1
3
4
230
9
1
1
1
1
1
1
1
1
1
1
10
175
10
1
1
1
1
1
1
1
1
8
6000
6000
6000
6000
6000
6000
6000
6000
6000
5232
100.00
100.00
100.00
100.00
100.00
100.00
100.00
100.00
100.00
87.20
100.00
C
1304
1
2
2
2
6
978
2
2
2
2
1
2
2
1
12
843
3
1
1
4
3
3
3
3
18
702
4
2
2
1
1
1
1
8
661
5
4
4
1
1
10
504
6
1
1
1
1
4
440
7
1
1
4
1
2
3
12
319
8
1
1
2
4
230
9
1
1
1
1
3
2
1
10
175
10
2
2
1
2
1
8
6000
6000
6000
6000
6000
6000
6000
6000
6000
5232
100.00
100.00
100.00
100.00
100.00
100.00
100.00
100.00
100.00
87.20
100.00
D
1304
1
2
2
2
6
978
2
1
1
1
3
3
3
12
843
3
1
2
2
1
1
1
1
5
4
18
702
4
1
7
8
661
5
3
3
2
2
10
504
6
4
4
440
7
5
4
3
12
319
8
2
1
1
4
230
9
1
1
1
1
1
1
1
3
10
175
10
1
1
6
8
5999
5996
5996
5990
5990
5987
5977
5975
5974
5348
99.98
99.93
99.93
99.83
99.83
99.78
99.62
99.58
99.57
89.13
99.79
E
1304
1
2
2
2
6
978
2
2
2
2
1
1
1
1
1
1
12
843
3
4
4
4
4
2
18
702
4
1
1
1
2
2
1
8
661
5
1
1
1
1
3
3
10
504
6
1
1
1
1
4
440
7
1
1
1
1
2
2
4
12
319
8
1
1
1
1
4
230
9
1
1
1
1
1
1
1
1
1
1
10
175
10
3
3
2
8
6000
6000
6000
6000
6000
6000
6000
6000
6000
5232
100.00
100.00
100.00
100.00
100.00
100.00
100.00
100.00
100.00
87.20
100.00
In the following tables the columns indicate the bins (i) whereas the rows indicate the items (j). The first row below the tables belongs to the per an item . The second one indicates the rate of fullness of the bin related to the column . The gray cells are the optimum solutions.
Table 4 includes the comparison of the software with the other packages in terms of CPU time. As it is seen, the software has the best CPU time for each problems. When we compare the other packages of B, C and E which are equivalent related to their solution quality and the software, it is seen that the software is 1.65 times more efficient than C which is the closest competitor according to the rate of time over solution. Computational experiments run through Intel Pentium 4 CPU 2.40 GHz and 512 MB RAM devised computer.
PI
PII
bbkp
51
39
A
60
40
B
135
363
C
91
64
D
702
1010
E
2150
2622
The screenshots of the software bbkp for the problems PI and PII are shown in Figs. 3 and 4, respectively.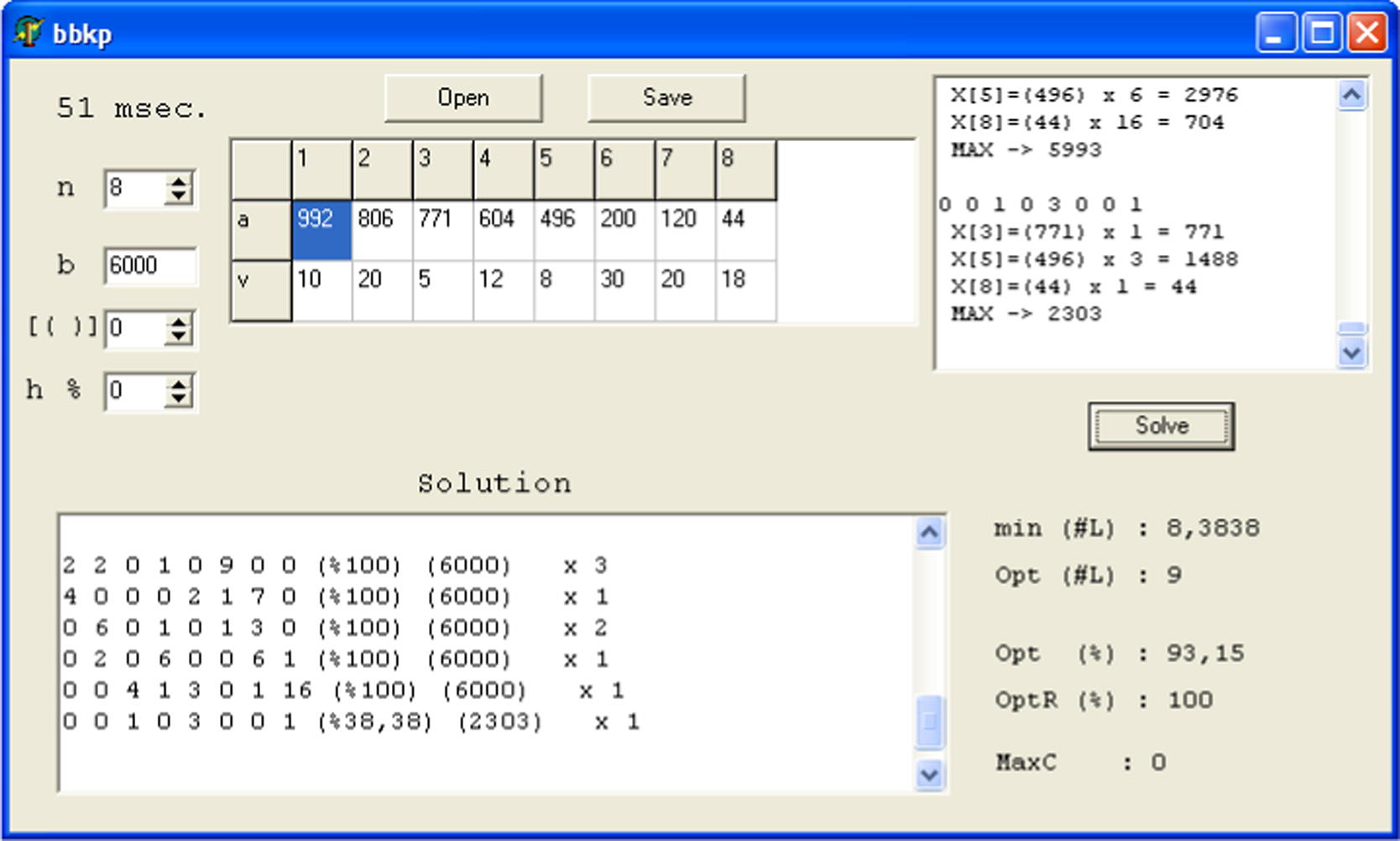
The screenshot of bbkp for PI.
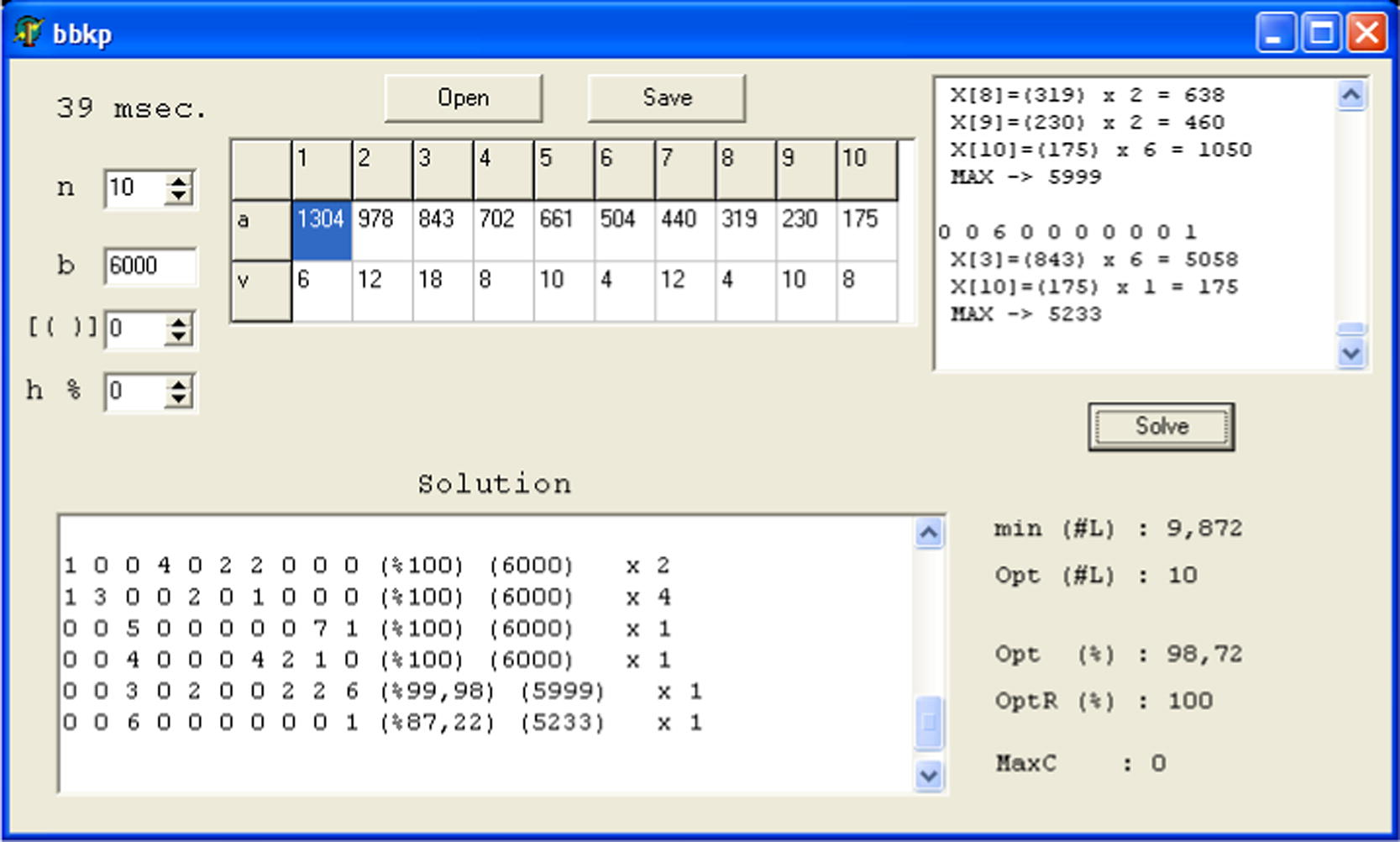
The screenshot of bbkp for PII.
5 Conclusion
A new mathematical model for 1D-CSP is proposed and a new algorithm is developed relating this model. The algorithm is coded with Delphi and then by computational experiments with the real-life constraint optimization problems, and the obtained results are compared with the other 1D-CSP commercial packages. The computational experiments show the efficiency of the algorithm. For the time being, the Turkish version of this paper and the demo of the software are available through the link <http://sci.ege.edu.tr/∼math/projects/bbkp/>.
References
- Belov, G., 2003. Problems, Models and Algorithms in One- and Two-Dimensional Cutting. Technischen Universität Dresden.
- Computers and Intractability: A Guide to the Theory of NP-Completeness. San Francisco: W.H. Freeman & Co.; 1979.
- A linear programming approach to the cutting stock problem. Operat. Res.. 1961;9:849-859.
- [Google Scholar]
- A linear programming approach to the cutting stock problem, part II. Operat. Res.. 1963;11:863-888.
- [Google Scholar]
- Knapsack Problems. Berlin: Springer; 2004.
- Knapsack Problems: Algorithms and Computer Implementations. John Wiley & Sons; 1990.
- Nuriyev, U.G., Berberler, M.E., Gürsoy, A., Kaya, O., 2007. Preparation of a software package for one-dimensional cutting stock problem and application to the PVC, metal and public sector. “Inno-Venture 2007” Project Market, Tubitak, Ebiltem, Turkcell (Project Number BIT_208), İzmir, December 13–14.
- Nuriyev, U.G., Berberler M.E., Gürsoy A., 2008. Preparation of a software package for one-dimensional cutting stock problem and application to the PVC, metal and public sector. Project Market 2008, June 18. İzmir Institute of Technology, İzmir, p. 25.
- An improved tabu search approach with mixed objective function for one-dimensional cutting stock problems. Adv. Eng. Software. 2006;37(8):502-513.
- [Google Scholar]
Further reading
- [bbkp] (Bir Boyutlu Kesme Programı). <http://sci.ege.edu.tr/∼math/projects/bbkp/>.
- [A] (1D Stock Cutter). <http://www.astrokettle.com/pr1dsc.html>.
- [B] (Optimum Cut). <http://www.downloadjunction.com/product/software/30836/>.
- [C] (Real Cut 1D). <http://www.softplatz.com/Soft/Graphics/CADs/Real-Cut-1D.html>.
- [D] (Pipe Cutting Suite 3.11). <http://www.shareup.com/Pipe_Cutting_Suite-download-7887.html>.
- [E] (Cut Logic). <http://www.softpicks.net/software/CutLogic-1D-9970.htm>.







